Question

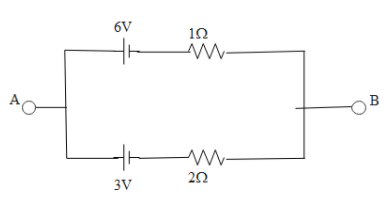
Two batteries of different EMFs and different internal resistance are connected as shown. The voltage across AB in volts is:

A. 4
B. 5
C. 6
D. 7

Answer 1

Hint: When we talk about small microcircuits, minute change in the internal resistance makes a huge difference in the quantities of the circuit. When cells are connected to each other in series the current flows from the higher potential to the low potential and it becomes necessary to calculate the average potential between any two points. This can be calculated with the help of a potentiometer which works as an external variable resistance applied to the circuit.
As per the given data
EMF of one cell (${{E}_{1}}$) is $6V$
The internal resistance of ${{E}_{1}}$ (${{r}_{1}}$) is $1\Omega $
EMF of another cell (${{E}_{2}}$) is $3V$
The internal resistance of ${{E}_{2}}$ (${{r}_{1}}$) is $2\Omega $

Formula used:
${{V}_{AB}}=\dfrac{\Sigma \dfrac{E}{r}}{\Sigma \dfrac{1}{r}}$

Complete answer:
Here the two cells or different internal resistance are connected to one other with the positive terminal. The current tends to follow from the higher potential to the lower potential.
The voltage between the terminals A and B can be given as,
${{V}_{AB}}=\dfrac{\Sigma \dfrac{E}{r}}{\Sigma \dfrac{1}{r}}$
By putting the values as per the given data,
$\begin{align}
  & {{V}_{AB}}=\dfrac{6+\dfrac{3}{2}}{1+\dfrac{1}{2}} \\
 & \\
 & \Rightarrow {{V}_{AB}}=\dfrac{\dfrac{15}{2}}{\dfrac{3}{2}} \\
 & \\
 & \Rightarrow {{V}_{AB}}=\dfrac{15}{2}\times \dfrac{2}{3} \\
 & \\
 & \Rightarrow {{V}_{AB}}=5V \\
\end{align}$
Thus the voltage across points A and B is \[{{V}_{AB}}=5V\].

And the correct option which represents the true value of the voltage between the points for the given question is Option B.

Note:
The voltage drop across a circuit is dependent on the total resistance across the circuit. According to the ohms’ law, it is said that voltage drop is directly proportional to the current flowing in the circuit. For complex circuits, the internal resistance of the cell is considered to be zero.