Question

How many triangles are possible given \[m\angle B = {33^ \circ },a = 27,b = 22\]?

Answer 1

Hint: Here we will first form a triangle with two known sides and one known angle. Then we will use the law of sine formula and get the value of one of the unknown angles. Then we will use the angle sum property of the triangle to find the third angle. Then using the obtained values and sine rule we will find the unknown side of the triangle. Finally, we will conclude how many triangles can be formed by the given data.

Complete step by step solution:
It is given that \[\angle B = {33^ \circ },a = 27,b = 22\]
So, let us form a $\vartriangle ABC$ using the given data.

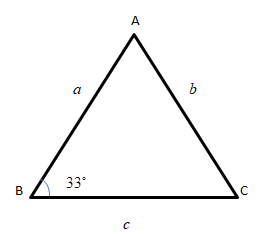
Now we will use Law of sine where,
\[\dfrac{{\sin A}}{a} = \dfrac{{\sin B}}{b} = \dfrac{{\sin C}}{c}\]……\[\left( 1 \right)\]
Taking the first two ratios, we get
\[\dfrac{{\sin A}}{a} = \dfrac{{\sin B}}{b}\]
Substituting \[\angle B = {33^ \circ },a = 27\] and \[b = 22\] in above equation, we get
\[ \Rightarrow \dfrac{{\sin A}}{{27}} = \dfrac{{\sin {{33}^ \circ }}}{{22}}\]
Multiplying the terms, we get
\[ \Rightarrow \sin A = \dfrac{{\sin {{33}^ \circ }}}{{22}} \times 27\]
Using the calculator, we will find the value of sine and substitute above and get,
\[\begin{array}{l} \Rightarrow \sin A = \dfrac{{0.544 \times 27}}{{22}}\\ \Rightarrow \sin A = 0.6684\end{array}\]
Now taking the sine inverse on both sides, we get
\[ \Rightarrow A = {\sin ^{ - 1}}\left( {0.6684} \right)\]
Using calculator get the value of sine inverse as,
\[ \Rightarrow A = {41.94^ \circ } \approx {42^ \circ }\]…………………\[\left( 2 \right)\]
Now as we know the sum of all angles of a triangle is \[{180^ \circ }\].
So,\[\angle A + \angle B + \angle C = {180^ \circ }\]
Substituting the value in above formula we get,
\[\begin{array}{l} \Rightarrow {42^ \circ } + {33^ \circ } + \angle C = {180^ \circ }\\ \Rightarrow \angle C = {180^ \circ } - {42^ \circ } - {33^ \circ }\end{array}\]
Subtracting the terms, we get
\[\angle C = {105^ \circ }\]…….\[\left( 3 \right)\]
Now using the last two ratios of equation \[\left( 1 \right)\], we get,
 \[\dfrac{{\sin B}}{b} = \dfrac{{\sin C}}{c}\]
Substituting the value of \[b,\angle B,\angle C\] in above ratio, we get
\[ \Rightarrow \dfrac{{\sin {{42}^ \circ }}}{{27}} = \dfrac{{\sin {{105}^ \circ }}}{c}\]
On cross multiplication, we get
\[ \Rightarrow c = \dfrac{{\sin {{105}^ \circ }}}{{\sin {{42}^ \circ }}} \times 27\]
Using the calculator, we get
\[ \Rightarrow c = \dfrac{{0.965}}{{0.669}} \times 27\]
Multiplying the terms, we get
\[ \Rightarrow c = 38.95 \approx 39\]……\[\left( 4 \right)\]
So, we get the values as :
\[\angle B = {33^ \circ },a = 27,b = 22\], \[\angle A = {42^ \circ },\angle C = {105^ \circ },c = 39\]
There is only one possible triangle with the above data.

Note:
A triangle is a two dimensional geometric figure that has 3 sides and three vertices. The Law of sine states that the ratio of the side of a triangle to the sine of opposite side angles are in the same ratio for all. This statement holds true for all sides and all angles irrespective of the difference in their length or angle. This law is generally used to find the length of the side or the angle of the triangle.