
To trace the required parabola:
${{(x-4y)}^{2}}=51y$
Answer
609.9k+ views
Hint: To solve this problem, one needs to be aware about the generalised equation of a parabola. This equation is given by ${{\left( \dfrac{px+qy+r}{\sqrt{{{p}^{2}}+{{q}^{2}}}} \right)}^{2}}=4a\left( \dfrac{lx+my+n}{{{l}^{2}}+{{m}^{2}}} \right)$. Here, a is the focus of the parabola. Further; p, q, r, l, m and n are the constants which will one comes across as the equation is solved. We will compare this equation with one given in the problem to trace the parabola to get the value of these constants.
Complete step-by-step answer:
To solve this problem, one must be aware about the general equation of parabola in detail. Generally, one is aware about the equation ${{y}^{2}}=4ax$ where there is no xy term (Here, a is the length of the focus of the parabola). However, in this problem as we expand the terms of the question, there will be a xy term, thus we make use of a different generalised equation. Thus, first to begin with, we expand the terms, we get,
${{(x-4y)}^{2}}=51y$
${{x}^{2}}+16{{y}^{2}}-8xy=51y$
Now, we try to compare with the below equation –
${{\left( \dfrac{px+qy+r}{\sqrt{{{p}^{2}}+{{q}^{2}}}} \right)}^{2}}=4a\left( \dfrac{lx+my+n}{{{l}^{2}}+{{m}^{2}}} \right)$-- (1)
Now, to start solving, we use a small trick, we introduce a variable (in this case k). To explain,
${{(x-4y+k)}^{2}}=51y+2kx-8ky+{{k}^{2}}$
(Thus, to make the equation to compare to (1), we do this manipulation. Also, since, we have added k in the square term on LHS, we have to subsequently add the terms on RHS for equality to hold true.)
${{(x-4y+k)}^{2}}=2kx+(51-8k)y+{{k}^{2}}$ -- (A)
Thus, we have two line equations –
x-4y+k=0 -- (2)
2kx+(51-8k)y+${{k}^{2}}$=0 -- (3)
These lines are perpendicular to each other since these are the equations of the axis and line perpendicular to the axis passing through the vertices of the parabola.
Let slope of (2) be m and slope of (3) be n. Thus,
m=$\dfrac{1}{4}$
n=\[\left( \dfrac{-2k}{51-8k} \right)\]
We have mn=-1 (condition of perpendicular lines)
Thus,
$\Rightarrow$ $\dfrac{1}{4}\times \left( \dfrac{-2k}{51-8k} \right)$=-1
Solving, we get,
$\begin{align}
& -2k=-4(51-8k) \\
& -2k=-204+32k \\
& 34k=204 \\
& k=6 \\
\end{align}$
We put this value in (A), we get,
\[\begin{align}
& {{(x-4y+6)}^{2}}=12x+(51-48)y+36 \\
& {{(x-4y+6)}^{2}}=12x+3y+36 \\
& {{(x-4y+6)}^{2}}=3(4x+y+12) \\
& {{(x-4y+6)}^{2}}=4\times \dfrac{3}{4}\times (4x+y+12) \\
& {{\left( \dfrac{x-4y+6}{\sqrt{17}} \right)}^{2}}=4\times \dfrac{3}{4}\times \dfrac{1}{\sqrt{17}}\times \dfrac{(4x+y+12)}{\sqrt{17}} \\
\end{align}\]
Thus, we can finally compare this to (1)
${{\left( \dfrac{px+qy+r}{\sqrt{{{p}^{2}}+{{q}^{2}}}} \right)}^{2}}=4a\left( \dfrac{lx+my+n}{{{l}^{2}}+{{m}^{2}}} \right)$
We can find, the constants value by comparing,
p=1, q=-4, r=6, a=$\dfrac{3}{4\sqrt{17}}$, l=4, m=1, n=12
To get the vertices, we have to solve the equations
x-4y+6=0 and 4x+y+12=0
Solving, we get,
x=$\dfrac{-54}{17},y=\dfrac{12}{17}$
Thus, the required parabola will have the above vertices with axis as x-4y+6=0. This will look as –
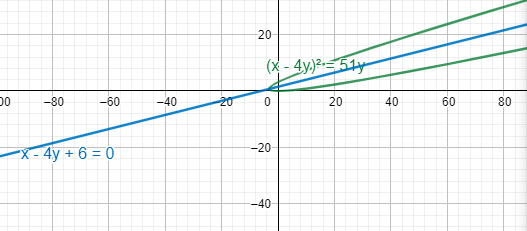
Note: While solving questions related to parabola apart from the familiar equation ${{y}^{2}}=4ax$, we should also be aware of the general equation of the parabola given by ${{\left( \dfrac{px+qy+r}{\sqrt{{{p}^{2}}+{{q}^{2}}}} \right)}^{2}}=4a\left( \dfrac{lx+my+n}{{{l}^{2}}+{{m}^{2}}} \right)$. This equation is especially useful when parabola involves xy terms in its equation.
Complete step-by-step answer:
To solve this problem, one must be aware about the general equation of parabola in detail. Generally, one is aware about the equation ${{y}^{2}}=4ax$ where there is no xy term (Here, a is the length of the focus of the parabola). However, in this problem as we expand the terms of the question, there will be a xy term, thus we make use of a different generalised equation. Thus, first to begin with, we expand the terms, we get,
${{(x-4y)}^{2}}=51y$
${{x}^{2}}+16{{y}^{2}}-8xy=51y$
Now, we try to compare with the below equation –
${{\left( \dfrac{px+qy+r}{\sqrt{{{p}^{2}}+{{q}^{2}}}} \right)}^{2}}=4a\left( \dfrac{lx+my+n}{{{l}^{2}}+{{m}^{2}}} \right)$-- (1)
Now, to start solving, we use a small trick, we introduce a variable (in this case k). To explain,
${{(x-4y+k)}^{2}}=51y+2kx-8ky+{{k}^{2}}$
(Thus, to make the equation to compare to (1), we do this manipulation. Also, since, we have added k in the square term on LHS, we have to subsequently add the terms on RHS for equality to hold true.)
${{(x-4y+k)}^{2}}=2kx+(51-8k)y+{{k}^{2}}$ -- (A)
Thus, we have two line equations –
x-4y+k=0 -- (2)
2kx+(51-8k)y+${{k}^{2}}$=0 -- (3)
These lines are perpendicular to each other since these are the equations of the axis and line perpendicular to the axis passing through the vertices of the parabola.
Let slope of (2) be m and slope of (3) be n. Thus,
m=$\dfrac{1}{4}$
n=\[\left( \dfrac{-2k}{51-8k} \right)\]
We have mn=-1 (condition of perpendicular lines)
Thus,
$\Rightarrow$ $\dfrac{1}{4}\times \left( \dfrac{-2k}{51-8k} \right)$=-1
Solving, we get,
$\begin{align}
& -2k=-4(51-8k) \\
& -2k=-204+32k \\
& 34k=204 \\
& k=6 \\
\end{align}$
We put this value in (A), we get,
\[\begin{align}
& {{(x-4y+6)}^{2}}=12x+(51-48)y+36 \\
& {{(x-4y+6)}^{2}}=12x+3y+36 \\
& {{(x-4y+6)}^{2}}=3(4x+y+12) \\
& {{(x-4y+6)}^{2}}=4\times \dfrac{3}{4}\times (4x+y+12) \\
& {{\left( \dfrac{x-4y+6}{\sqrt{17}} \right)}^{2}}=4\times \dfrac{3}{4}\times \dfrac{1}{\sqrt{17}}\times \dfrac{(4x+y+12)}{\sqrt{17}} \\
\end{align}\]
Thus, we can finally compare this to (1)
${{\left( \dfrac{px+qy+r}{\sqrt{{{p}^{2}}+{{q}^{2}}}} \right)}^{2}}=4a\left( \dfrac{lx+my+n}{{{l}^{2}}+{{m}^{2}}} \right)$
We can find, the constants value by comparing,
p=1, q=-4, r=6, a=$\dfrac{3}{4\sqrt{17}}$, l=4, m=1, n=12
To get the vertices, we have to solve the equations
x-4y+6=0 and 4x+y+12=0
Solving, we get,
x=$\dfrac{-54}{17},y=\dfrac{12}{17}$
Thus, the required parabola will have the above vertices with axis as x-4y+6=0. This will look as –

Note: While solving questions related to parabola apart from the familiar equation ${{y}^{2}}=4ax$, we should also be aware of the general equation of the parabola given by ${{\left( \dfrac{px+qy+r}{\sqrt{{{p}^{2}}+{{q}^{2}}}} \right)}^{2}}=4a\left( \dfrac{lx+my+n}{{{l}^{2}}+{{m}^{2}}} \right)$. This equation is especially useful when parabola involves xy terms in its equation.
Recently Updated Pages
What happens to glucose which enters nephron along class 10 biology CBSE

Write a dialogue with at least ten utterances between class 10 english CBSE

A circle is inscribed in an equilateral triangle and class 10 maths CBSE

When the JanmiKudian Act was passed that granted the class 10 social science CBSE

A sector containing an angle of 120 circ is cut off class 10 maths CBSE

The sum of digits of a two digit number is 13 If t-class-10-maths-ICSE

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the missing number in the sequence 259142027 class 10 maths CBSE




