Question

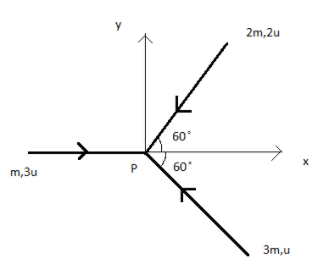
Three masses m, 2m, 3m are moving in a x-y plane with speed 3u, 2u and u respectively as shown in the figure. The three masses collide at point P and stick together. The velocity of the resulting mass will be:

(A)$\dfrac{u}{12}(\hat{i}+\sqrt{3}\hat{j})$
(B)$\dfrac{u}{12}(\hat{i}-\sqrt{3}\hat{j})$
(C)$\dfrac{u}{12}(-\hat{i}+\sqrt{3}\hat{j})$
(D)$\dfrac{u}{12}(-\hat{i}-\sqrt{3}\hat{j})$

Answer 1

Hint: This is a problem where collision is involved. In such a case we use the conservation of momentum and energy principles. But since it is not mentioned if it is elastic or an inelastic collision, we only use the conservation of momentum principle to solve this problem.
Formula used:
The conservation of momentum law gives us the following:
${{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}+{{m}_{3}}{{u}_{3}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}+{{m}_{3}}{{v}_{3}}$

Complete answer:
Let the masses of the three bodies be ${{m}_{1}}$ , ${{m}_{2}}$ and ${{m}_{3}}$ and the initial velocities be given by u and the final velocities be given by v for the three different masses.
Now, applying the conservation of momentum principle, we have
${{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}+{{m}_{3}}{{u}_{3}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}+{{m}_{3}}{{v}_{3}}$ .................. (1)
Given,
${{m}_{1}}=m$
${{m}_{2}}=2m$
${{m}_{3}}=3m$
And the initial velocities be given by
${{u}_{1}}=3u$
${{u}_{2}}=2u$
${{u}_{3}}=u$
Also, the three masses after colliding stick together, so the final mass is given by the sum of the masses of the three bodies.
Thus, plugging these values of mass and velocities in equation (1), and resolving the velocity into parallel and perpendicular components, we have
$\Rightarrow m\times 3u\hat{i}+2m\times 2u(-\hat{i}\cos 60-\hat{j}\sin 60)+3m\times u(-\hat{i}\cos {{60}^{\circ }}+\hat{j}\sin {{60}^{\circ }})=(m+2m+3m)v$
 Where, v is the value of final velocity.
Solving the equation and simplifying we have,
$\Rightarrow \vec{v}=\dfrac{u}{12}(-\hat{i}-\sqrt{3}\hat{j})$
Thus the correct value of velocity after collision is given by $\dfrac{u}{12}(-\hat{i}-\sqrt{3}\hat{j})$.

So the correct option is (D) $\dfrac{u}{12}(-\hat{i}-\sqrt{3}\hat{j})$ .

Additional Information:
In problems involving collision we always consider the conservation of energy and conservation of momentum to solve the question using the appropriate information. In case of elastic collisions, energy is conserved along with momentum whereas in case of non-elastic collisions only conservation of momentum is applied.

Note:
Whenever there arises problems with collisions we consider the conservation of momentum principle as we have in this problem. While applying this principle we do not have to deduce if the collision is elastic or in-elastic. The principle is valid either wise. Another important thing to note here is that while calculating momentum, the velocity needs to be split into its two component forms. Keeping these two points in mind, we can easily solve such questions.