Question

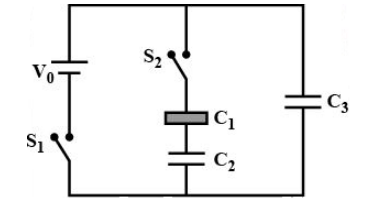
Three identical capacitors \[{C_1}\], \[{C_2}\] and \[{C_3}\] have a capacitance of \[1\mu F\]each and they are uncharged initially. They are connected in a circuit as shown in the figure and \[{C_1}\] ​ is then filled completely with a dielectric material of relative permittivity \[{ \in _r}\] ​. The cell electromotive force (emf) \[{V_o} = 8V\]. First, the switch \[{S_1}\] ​ is closed while the switch \[{S_2}\] is kept open. When the capacitor \[{C_3}\] is fully charged, \[{S_1}\] ​ is opened and \[{S_2}\] is closed simultaneously. When all the capacitors reach equilibrium, the charge on \[{C_3}\] ​ is found to be \[5\mu C\]. The value of \[4 \times { \in _r}\]is:

Answer 1

Hint: Find the charge distribution of the capacitors in both the scenarios, i.e. when the switch \[{S_1}\]is closed and the other switch is open. Similarly find the distribution of charges on the capacitors when the switch \[{S_2}\]is closed and the other switch is open. Then apply Kirchhoff’s law to find the required answer.

Complete answer:
If we consider the case when the switch \[{S_1}\] is closed, then we get a circuit as-

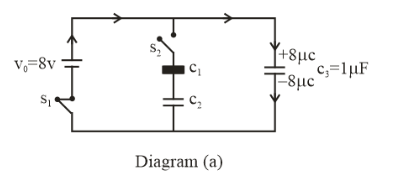
The charge on the capacitor \[{C_3}\] will be = \[C \times V\]= \[1 \times 8 = 8\mu C\], as shown in the figure above. This happened because all the charge travelling from the voltage source has travelled to the capacitor and it has stored charge up to its maximum level.

Now when the capacitor \[{C_3}\]is charged and now we are opening switch \[{S_1}\]and closing the middle switch \[{S_2}\], some charge distribution will take place and as all the capacitors are identical, so \[{C_1}\] and \[{C_2}\]will have a capacitance of \[3\mu C\]each. This is because after closing the switch \[{S_2}\], the value of capacitance of \[{C_3}\]must be \[5\mu C\]as given in the question. The diagram of the new circuit is as follows-

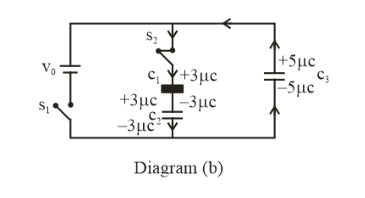
Now in the capacitor \[{C_1}\]there is a dielectric medium of relative permittivity \[{ \in _r}\], so by applying Kirchhoff’s law we get that-
\[ \dfrac{{{q_1}}}{{{C_1}{ \in _r}}} + \dfrac{{{q_2}}}{{{C_2}}} = \dfrac{{{q_3}}}{{{C_3}}}\]
Now as charge and capacitance are same because of their identical nature so,
\[ \Rightarrow \dfrac{3}{1}\left( {1 + \dfrac{1}{{{ \in _r}}}} \right) = \dfrac{5}{1}\]
\[ \therefore { \in _r} = 1.5\]

Therefore the value of \[4 \times { \in _r}\]= \[6\].

Note:Relative permittivity is basically the ratio of the capacitance of a capacitor using that material as a dielectric, compared with a similar capacitor that has vacuum as its dielectric. Different kinds of dielectric material will give different conditions.