Question

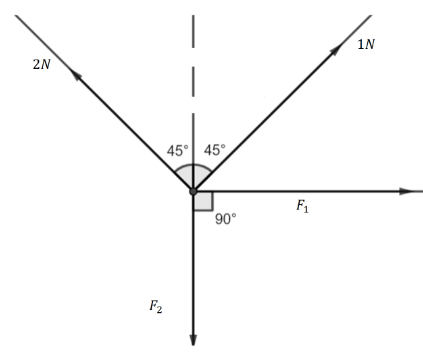
There are four forces acting at a point P produced by strings as shown in figure, which is at rest. The forces \[{F_1}\] and \[{F_2}\] are:

A. \[\dfrac{1}{{\sqrt 2 }}N,\dfrac{3}{{\sqrt 2 }}\,N\]
B. \[\dfrac{3}{{\sqrt 2 }}N,\dfrac{1}{{\sqrt 2 }}\,N\]
C. \[\dfrac{1}{{\sqrt 2 }}N,\dfrac{1}{{\sqrt 2 }}\,N\]
D. \[\dfrac{3}{{\sqrt 2 }}N,\dfrac{3}{{\sqrt 2 }}\,N\]

Answer 1

Hint:When a body is at rest according to Newton’s law the net force acting on the body is zero. Since, Newton’s first law states that if a body is at rest or moving with uniform velocity the body will be at rest or will keep moving with uniform speed or velocity if no external force is applied to it.

Formula used:
The net force acting on the body is given by Newton’s second law as,
\[F = ma\]
Where \[F\] is the force acting on the body \[m\] is the mass of the body and \[a\] is the acceleration of the body.
The net force acting on a body at equilibrium, \[{F_{Net}} = 0\].

Complete step by step answer:
We have given here from the diagram four forces being applied to a body. Now, to find the value of the forces \[{F_1}\] and \[{F_2}\]we have to find the component of the forces \[1\,N\]and \[2\,N\]along the unknown forces.

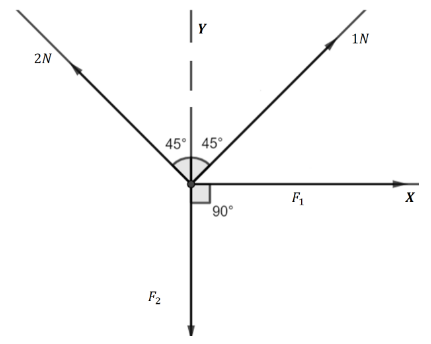
So, the components of \[1N\]along the X-axis and Y-axis are \[1\,N\sin {45^ \circ }\] and \[1\,N\cos {45^ \circ }\] respectively. Now components of \[2\,N\] along the negative X-axis and Y-axis are \[2\,N\sin {45^ \circ }\] and \[2\,N\cos {45^ \circ }\]respectively. Now, to keep the body at rest all components of force acting along both the axes must be equal.HEcne, we can write for X-component,
\[{F_1} - 2\sin {45^ \circ } + 1\sin {45^ \circ } = 0\]
\[\Rightarrow {F_1} - 2\dfrac{1}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 2 }} = 0\]
\[\Rightarrow {F_1} = \dfrac{1}{{\sqrt 2 }}\]
For, y-component we can write,
\[{F_2} - 2\cos {45^ \circ } - 1\cos {45^ \circ } = 0\]
\[\Rightarrow {F_2} - 2\dfrac{1}{{\sqrt 2 }} - \dfrac{1}{{\sqrt 2 }} = 0\]
\[\therefore {F_2} = \dfrac{3}{{\sqrt 2 }}\]
Hence, the value of \[{F_1}\]is \[\dfrac{1}{{\sqrt 2 }}N\] and the value of\[{F_2}\] is \[\dfrac{3}{{\sqrt 2 }}N\].

Hence, option A is the correct answer.

Note: To solve this type of problem remember that the net force at equilibrium is always zero and always from the given forces divide each force into components and equate them to find the value of the unknown forces.