Question

The vertices of a rhombus are \[\left( { - 5,0} \right),\left( {0,8} \right),\left( {5,0} \right)\& \left( {0, - 8} \right)\] . the product of the lengths of its diagonals is
A.40
B.80
C.160
D.120

Answer 1

Hint: Students don’t panic by seeing so much data! This is very simple to solve. But first we will plot the points in order to know the end points of the diagonals. Then we will go to find the distance or length of the diagonal and at the end the actual problem that is the product of the diagonals.

Complete step-by-step answer:
Now we are given four points. These are the vertices of the rhombus given. We will plot these points first.

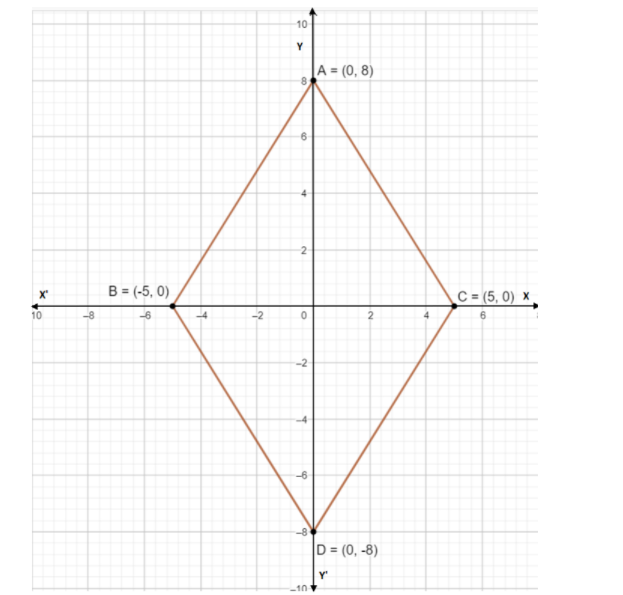
Now we can see the end points of the diagonals. So we will measure the length of the diagonal. We have done this before in the very starting chapters of the number line. Now we will just measure the distance as the units between the vertices on Y axis and the same on X axis.
On observing the graph, we came to notice that the distance between vertices A and D is 16 units that is from 8 to -8. This is the length of the diagonal.
On the other hand the distance between vertices B and C is 10 units that is from -5 to 5. This is the length of the other diagonal.
Now we have found the distances as 10 and 16 units. So the product of the lengths will be,
\[{d_1} \times {d_2} = 10 \times 16 = 160\]
Thus the correct option is C.
So, the correct answer is “Option C”.

Note: Note that we can solve the same problem by using the distance formula \[d = \sqrt {{{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{x_2} - {x_1}} \right)}^2}} \].
But since one of the coordinates of the vertices is zero we can easily find the length by measuring the unit distances so we used it here. But if the vertices given have both the coordinates given then definitely go for the distance formula.