Question

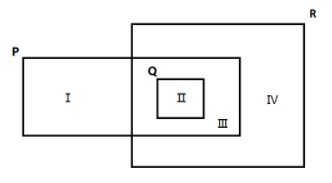
The Venn diagram shows sets \[P\], \[Q\] and \[R\]with regions labelled, Ⅰ, Ⅱ, Ⅲ and Ⅳ. State the regions which represents set \[\left[ {P \cap {{\left( {Q \cup R} \right)}^\prime }} \right]\]

1) Ⅰ
2) Ⅱ
3) Ⅲ
4) Ⅳ

Answer 1

Hint: Firstly, find the region of the inside bracket,\[\left( {Q \cup R} \right)\] which includes the region including both \[Q\] and \[R\]. Next, take the compliment of the region \[\left( {Q \cup R} \right)\] by excluding the region \[\left( {Q \cup R} \right)\] from the universal set or all regions. Lastly, solve \[\left[ {P \cap {{\left( {Q \cup R} \right)}^\prime }} \right]\] by taking the common region of set \[P\]and compliment of \[\left( {Q \cup R} \right)\] to find the required region.

Complete step by step solution: We can determine the region \[\left( {Q \cup R} \right)\] by finding the union of \[Q\] with\[R\], that is the region which includes both the sets \[Q\] and \[R\].
As, it is seen from the diagram, region Ⅱ, Ⅲ and Ⅳ includes the set \[Q\] and \[R\].
Next, take the compliment of the region \[\left( {Q \cup R} \right)\], that is, take the region excluding Ⅱ , Ⅲ and Ⅳ from the given diagram.
The region left after excluding the region Ⅱ, Ⅲ and Ⅳ is region Ⅰ.
We can see from the diagram, set \[P\]includes region Ⅰ, Ⅱ and Ⅲ.
Now, to solve the expression \[\left[ {P \cap {{\left( {Q \cup R} \right)}^\prime }} \right]\] take the intersection of set \[P\] and \[{\left( {Q \cup R} \right)^\prime }\], that is take the region with is common in set \[P\] and \[{\left( {Q \cup R} \right)^\prime }\].
The region Ⅰ is the common region of set \[P\] and \[{\left( {Q \cup R} \right)^\prime }\].
Hence, \[\left[ {P \cap {{\left( {Q \cup R} \right)}^\prime }} \right]\] represents region Ⅰ.

Note: Students often get confused with the symbols of union and intersection. \[ \cup \] represents union between two sets and \[ \cap \] represents intersection of the two sets. Identify the regions corresponding to the sets correctly. A single set may include more than one regions. Also, look at the given Venn diagram carefully before selecting the region.