Question

The tops of two poles of heights 20m and 14m are connected by a wire if the wire makes an angle of \[{{30}^{0}}\]with the horizontal then the length of wire is.
(a) 40m
(b) 12m
(c) 28m
(d) 68m

Answer 1

Hint: We solve this problem first by drawing the respected figure with the information given as follows

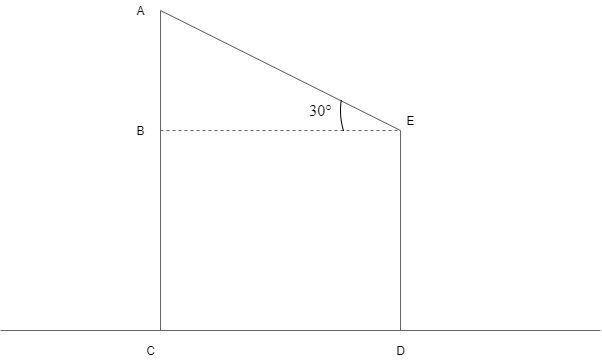
Here, we find the length of wire AE by sing the formula of sine of angle given as
 \[\sin \theta =\dfrac{\text{opposite side to }\theta }{\text{hypotenuse}}\]from the triangle \[\Delta ABE\].

Complete step-by-step answer:
We are given that the heights of two towers are 20m and 14m.
From the figure we can write that
 \[\begin{align}
  & \Rightarrow AC=20m \\
 & \Rightarrow ED=14m \\
\end{align}\]
Here, we know that the angle \[\angle ABE={{90}^{0}}\]so, we can write
 \[\Rightarrow BC=ED=14m\]
Now we can divide the length AC as follows
 \[\Rightarrow AC=AB+BC\]
By substituting the required values in above equation we get
 \[\begin{align}
  & \Rightarrow 20m=AB+14m \\
 & \Rightarrow AB=6m \\
\end{align}\]
Now, let us consider the triangle \[\Delta ABE\]
We know that sine of angle given as
 \[\sin \theta =\dfrac{\text{opposite side to }\theta }{\text{hypotenuse}}\]
By using this formula to \[\angle AEB\]in the triangle \[\Delta ABE\]we get
 \[\Rightarrow \sin \left( \angle AEB \right)=\dfrac{AB}{AE}\]
We are given that the wire AE makes an angle of \[{{30}^{0}}\]with horizontal. So, we can write \[\angle AEB={{30}^{0}}\]
Now, by substituting the required values in above equation we get
 \[\begin{align}
  & \Rightarrow \sin \left( {{30}^{0}} \right)=\dfrac{6}{AE} \\
 & \Rightarrow AE=\dfrac{6}{\sin \left( {{30}^{0}} \right)} \\
\end{align}\]
We know that from the standard table of trigonometric functions \[\sin \left( {{30}^{0}} \right)=\dfrac{1}{2}\].
By substituting this value in above equation we get
 \[\begin{align}
  & \Rightarrow AE=\dfrac{6}{\left( \dfrac{1}{2} \right)} \\
 & \Rightarrow AE=6\times 2=12 \\
\end{align}\]
Therefore the length of wire is given as 12m.

So, the correct answer is “Option B”.

Note: Students may make mistakes in applying the formula of sine of an angle. The sine of an angle is given as
 \[\sin \theta =\dfrac{\text{opposite side to }\theta }{\text{hypotenuse}}\]
This formula is applicable only in case of right angles triangle because we have hypotenuse in right angled triangle only. But some students may apply this formula to all types of triangles which is a big mistake. Here, since the triangle \[\Delta ABE\]is right angles, we used this formula. So, the definitions of basic terms need to be taken care of.