Question

The tangents to the circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ having inclinations $\alpha \text{ and }\beta $ intersect at P. If $\cot \alpha +\cot \beta =0,$ then the locus of P is
(A) x + y = 0
(B) x – y = 0
(C) xy = 0
(D) None of these

Answer 1

Hint: Use equation of tangent formula from an external point to circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$. Form the quadratic and relate the roots with the coefficients of quadratic.

The given equation of circle is,
${{x}^{2}}+{{y}^{2}}={{a}^{2}}$……………….(1)
Two tangents having inclination $\alpha \text{ and }\beta $ which means they are making angles $\alpha \text{ and }\beta $ with x – axis intersecting at P as shown in diagram.
As centre of circle given is (O,O) and radius = a if we compare it with standard equation of circle
${{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{a}^{2}}$
Where $\left( {{x}_{1}},{{y}_{1}} \right)$ is centre and a is radius.

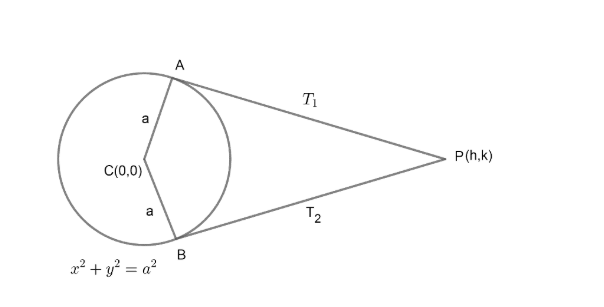
Let point P is (h, k) of which we have to find locus.
Now, we have two tangents ${{T}_{1}}\text{ and }{{T}_{2}}$ with inclinations $\alpha \text{ and }\beta $. Hence, slopes of tangents ${{T}_{1}}\text{ and }{{T}_{2}}$ be $\tan \alpha \text{ and tan}\beta $ as slope is tan of angle of any line with positive direction of x – axis.
We have given relation from question;
$\cot \alpha +\cot \beta =0$…………………… (2)
As, we know that tangent from any external point of circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ with slope given as m is ;
\[y=mx\pm a\sqrt{{{m}^{2}}+1}\] ………………. (3)
Where m is slope of tangent
a = radius of circle
Let us simplify equation (3) as;
$y-mx=\pm a\sqrt{{{m}^{2}}+1}$
Squaring both sides of above equation;
$\begin{align}
  & {{\left( y-mx \right)}^{2}}={{a}^{2}}\left( {{m}^{2}}+1 \right) \\
 & {{y}^{2}}+{{m}^{2}}{{x}^{2}}-2myx={{a}^{2}}{{m}^{2}}+{{a}^{2}} \\
\end{align}$
Rewriting the above equation with quadratic in ‘m’, we get;
${{m}^{2}}\left( {{a}^{2}}-{{x}^{2}} \right)+2myx+{{a}^{2}}-{{y}^{2}}=0$ ………………… (4)
Now, we have a quadratic in ‘m’ which means it will have two roots. Let ${{m}_{1}}\text{ and }{{m}_{2}}$ are roots of equation (4).
As tangents are drawn from an external point and only two tangents can be drawn from any external point to circle.
Let these slopes represent tangents ${{T}_{1}}\text{ and }{{T}_{2}}$, which has slope $\tan \alpha \text{ and tan}\beta $.
Hence, ${{m}_{1}}=\tan \alpha ,{{m}_{2}}=\tan \beta $ are roots of equation (4);
As we know, if we have quadratic $A{{x}^{2}}+Bx+C$, then
 $\begin{align}
  & \text{sum of roots }=\dfrac{-B}{A} \\
 & \text{product of roots = }\dfrac{C}{A} \\
\end{align}$
From equation (4), we get;
$\begin{align}
  & \tan \alpha +\text{tan}\beta =\dfrac{-2xy}{{{a}^{2}}-{{x}^{2}}} \\
 & \tan \alpha +\text{tan}\beta =\dfrac{{{a}^{2}}-{{y}^{2}}}{{{a}^{2}}-{{x}^{2}}} \\
\end{align}$
As, tangents ${{T}_{1}}\text{ and }{{T}_{2}}$ with slopes $\tan \alpha \text{ and tan}\beta $ are intersecting at (h, k). Hence, we can replace (x, y) by (h, k).
Therefore,
$\begin{align}
  & \tan \alpha +\text{tan}\beta =\dfrac{-2xy}{{{a}^{2}}-{{h}^{2}}}..............\left( 5 \right) \\
 & \tan \alpha +\text{tan}\beta =\dfrac{{{a}^{2}}-{{k}^{2}}}{{{a}^{2}}-{{h}^{2}}}...............\left( 6 \right) \\
\end{align}$
From equation (2), we have;
$\cot \alpha +\cot \beta =0$
We know that $\cot \theta =\dfrac{1}{\tan \theta }$
Hence,

$\begin{align}
  & \dfrac{1}{\tan \alpha }+\dfrac{1}{\tan \beta }=0 \\
 & \dfrac{\tan \alpha +\tan \beta }{\tan \alpha \tan \beta }=0 \\
 & \tan \alpha +\tan \beta =0............\left( 7 \right) \\
\end{align}$
Now, from equation (5), we have;
$\tan \alpha +\tan \beta =\dfrac{-2hk}{{{a}^{2}}-{{h}^{2}}}$ ……………….. (8)
From equation (7) & (8), we get;
$\begin{align}
  & \dfrac{-2hk}{{{a}^{2}}-{{h}^{2}}}=0 \\
 & hk=0 \\
\end{align}$
Now, replacing (h, k) by (x, y) to get locus;
xy = 0 (Required locus)
Hence, the correct answer is option (C).

Note: Another approach for this question would be that we can suppose point A and B as parametric coordinates. Point A as $\left( a\cos {{\theta }_{1}},b\sin {{\theta }_{1}} \right)$ and point B as $\left( a\cos {{\theta }_{2}},b\sin {{\theta }_{2}} \right)$.
Now, write equation of tangents through A and B as T = 0
Tangents through A and B as
$\begin{align}
  & \dfrac{x\cos {{\theta }_{1}}}{a}+\dfrac{y\sin {{\theta }_{1}}}{b}=1 \\
 & \dfrac{x\cos {{\theta }_{2}}}{a}+\dfrac{y\sin {{\theta }_{2}}}{b}=1 \\
\end{align}$
Hence, slope of tangents A and B is given as;
$\dfrac{\dfrac{-\cos {{\theta }_{1}}}{a}}{\dfrac{\sin {{\theta }_{1}}}{b}}=\dfrac{-\cos {{\theta }_{1}}}{a}\times \dfrac{b}{\sin {{\theta }_{1}}}=\dfrac{-b\cos {{\theta }_{1}}}{a\sin {{\theta }_{1}}}$
Similarly, tangents through B has
$slope=\dfrac{-b}{a}\dfrac{\cos {{\theta }_{2}}}{\sin {{\theta }_{2}}}$
We have slopes given as $\tan \alpha \text{ and tan}\beta $.
Hence, we have equations
$\begin{align}
  & \tan \alpha =\dfrac{-b}{a}\dfrac{\cos {{\theta }_{1}}}{\sin {{\theta }_{1}}}=\dfrac{-b}{a}\cot {{\theta }_{1}} \\
 & \tan \beta =\dfrac{-b}{a}\dfrac{\cos {{\theta }_{2}}}{\sin {{\theta }_{2}}}=\dfrac{-b}{a}\cot {{\theta }_{2}} \\
\end{align}$
Now, find intersection point (h, k) by solving equations of tangents written above try to eliminate ${{\theta }_{1}}\And {{\theta }_{2}}$ with the help of given relation $\cot \alpha +\cot \beta =0,$and given above i.e. $\tan \alpha =\dfrac{-b}{a}\cot {{\theta }_{1}},\tan \beta =\dfrac{-b}{a}\cot {{\theta }_{2}}$.
One can go wrong while writing the relations \[\tan \alpha +\tan \beta \]and \[\tan \alpha .\tan \beta \] from the quadratic ${{\left( y-mx \right)}^{2}}={{a}^{2}}\left( {{m}^{2}}+1 \right)$