Question

The tangent at a point $P$ on the hyperbola $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$ meets one of the directrix in $F$. If $PF$ subtends an angle $\theta $ at the corresponding focus, then \[\theta \] equals:
A.$\dfrac{\pi }{4}$
B.$\dfrac{\pi }{2}$
C.$\dfrac{{3\pi }}{4}$
D.$\pi $

Answer 1

Hint: We will first draw the diagram corresponding to the given condition. We will then find the coordinates of the points mentioned in the question. Then we will find the slope of lines that subtends the required angle. Next, we calculate the product of the slopes to determine the angle.

Complete step-by-step answer:
We are given that the equation of hyperbola is $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$

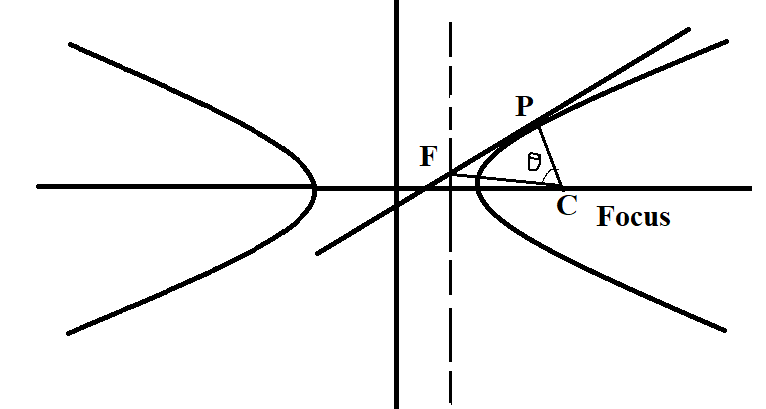
We have to find $\theta $
The normal form of any point on the hyperbola is of the form $\left( {a\sec \theta ,b\tan \theta } \right)$
$P$ is a point on hyperbola through which a tangent passes, then let $P$ be $\left( {a\sec \theta ,b\tan \theta } \right)$
We know that equation of tangent through a point $\left( {{x_1},{y_1}} \right)$ passing through a hyperbola is $\dfrac{{x{x_1}}}{{{a^2}}} - \dfrac{{y{y_1}}}{{{b^2}}} = 1$
Then, equation of tangent passing through point $P\left( {a\sec \theta ,b\tan \theta } \right)$ is
$\dfrac{{x\left( {a\sec \theta } \right)}}{{{a^2}}} - \dfrac{{y\left( {b\tan \theta } \right)}}{{{b^2}}} = 1$
$ \Rightarrow \dfrac{x}{a}\sec \theta - \dfrac{y}{b}\tan \theta = 1$ (1)
We are also given that the tangent passes through the directrix.
We know that equation of directrix is $x = \dfrac{a}{e}$
On substituting the value of $x = \dfrac{a}{e}$ in equation (1)
Hence,
 $
  \dfrac{{\dfrac{a}{e}}}{a}\sec \theta - \dfrac{y}{b}\tan \theta = 1 \\
   \Rightarrow \dfrac{{\sec \theta }}{e} - \dfrac{y}{b}\tan \theta = 1 \\
$
We will now find the value of $y$ from the above equation
$
  \dfrac{{\sec \theta }}{e} - 1 = \dfrac{y}{b}\tan \theta \\
  \left( {\dfrac{{\sec \theta }}{e} - 1} \right)\dfrac{b}{{\tan \theta }} = y \\
$
Therefore, the coordinates of focus are $\left( {ae,0} \right)$, the coordinates of $P$ are $\left( {a\sec \theta ,b\tan \theta } \right)$ and coordinates of $F$ are $\left( {\dfrac{a}{e},\left( {\dfrac{{\sec \theta }}{e} - 1} \right)\dfrac{b}{{\tan \theta }}} \right)$
We will know find the slope of $PC$ and slope of $FC$, where slope is given by $\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
Then, slope of $PC$ is
 $
  {m_1} = \dfrac{{b\tan \theta }}{{a\sec \theta - ae}} \\
   \Rightarrow {m_1} = \dfrac{{b\dfrac{{\sin \theta }}{{\cos \theta }}}}{{a\dfrac{1}{{\cos \theta }} - ae}} \\
   \Rightarrow {m_1} = \dfrac{{b\sin \theta }}{{a - ae\cos \theta }} \\
$
The slope of $FC$ is
$
  {m_2} = - \dfrac{{\left( {\dfrac{{\sec \theta }}{e} - 1} \right)\dfrac{b}{{\tan \theta }}}}{{\dfrac{a}{e} - ae}} \\
   \Rightarrow {m_2} = - \dfrac{{\dfrac{b}{e}\dfrac{{\dfrac{1}{{\cos \theta }}}}{{\dfrac{{\sin \theta }}{{\cos \theta }}}} - \dfrac{{b\cos \theta }}{{\sin \theta }}}}{{\dfrac{{a - a{e^2}}}{e}}} \\
   \Rightarrow {m_2} = - \dfrac{{\dfrac{b}{{e\sin \theta }} - \dfrac{{b\cos \theta }}{{\sin \theta }}}}{{\dfrac{{a - a{e^2}}}{e}}} \\
   \Rightarrow {m_2} = - \dfrac{{b - be\cos \theta }}{{\left( {a - a{e^2}} \right)\sin \theta }} \\
$
It is also known that ${b^2} = {a^2}\left( {1 - {e^2}} \right)$
Then,
$
  {m_2} = - \dfrac{{b\left( {1 - e\cos \theta } \right)}}{{a\dfrac{{{b^2}}}{{{a^2}}}\sin \theta }} \\
   \Rightarrow {m_2} = - \dfrac{{a\left( {1 - e\cos \theta } \right)}}{{b\sin \theta }} \\
$
Now, we will calculate ${m_1}.{m_2}$
Hence, \[\dfrac{{b\sin \theta }}{{a - ae\cos \theta }}\left( { - \dfrac{{a\left( {1 - e\cos \theta } \right)}}{{b\sin \theta }}} \right) = - 1\]
Since, ${m_1}{m_2} = - 1$, this implies $\theta = \dfrac{\pi }{2}$
Hence, option B is correct.

Note: Hyperbola is a conic section whose general equation is $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$. Use the formulas of trigonometry correctly. If the product of slopes of two lines is $ - 1$, then lines are perpendicular to each other. That is, the angle between them is ${90^ \circ }$