Question

The sum of real roots of the equation ${{x}^{2}}+5\left| x \right|+6=0$ is
A. 5
B. 10
C. -5
D. None of these.

Answer 1

Hint: Solve for cases when x>0 and $x\le 0$ individually and remove extraneous roots(means which does not satisfy two cases). Use property that |x| = x when x>0 and |x| = -x when $x\le 0$. Find the sum of all the real roots found. Alternatively, you can plot the given function and find the points at which the graph of the given function intersects the x-axis.

“Complete step-by-step answer:”
We will solve the above question for two cases.
Case I: x>0
We have |x| = x
$\Rightarrow {{x}^{2}}+5x+6=0$
Using the quadratic formula which states that for quadratic equation $a{{x}^{2}}+bx+c=0$ the roots are $x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$
Here a = 1, b = 5 and c = 6
Using the quadratic formula, we get
$\begin{align}
  & x=\dfrac{-5\pm \sqrt{{{5}^{2}}-4\left( 1 \right)\left( 6 \right)}}{2\left( 1 \right)} \\
 & \Rightarrow x=\dfrac{-5\pm \sqrt{25-24}}{2} \\
 & \Rightarrow x=\dfrac{-5\pm \sqrt{1}}{2}=\dfrac{-5\pm 1}{2} \\
 & \Rightarrow x=\dfrac{-5+1}{2}\text{ or }x=\dfrac{-5-1}{2} \\
 & \Rightarrow x=-2\text{ or }x=-3 \\
\end{align}$
Since x>0 both x = -2 and x = -3 are extraneous roots.
Case II: $x\le 0$
We have |x| = -x
$\Rightarrow {{x}^{2}}-5x+6=0$
Here a = 1, b = -5 and c = 6
Using the quadratic formula, we get
$\begin{align}
  & x=\dfrac{-\left( -5 \right)\pm \sqrt{{{\left( -5 \right)}^{2}}-4\left( 1 \right)\left( 6 \right)}}{2\left( 1 \right)} \\
 & \Rightarrow x=\dfrac{5\pm \sqrt{25-24}}{2} \\
 & \Rightarrow x=\dfrac{5\pm \sqrt{1}}{2}=\dfrac{5\pm 1}{2} \\
 & \Rightarrow x=\dfrac{5+1}{2}\text{ or }x=\dfrac{5-1}{2} \\
 & \Rightarrow x=3\text{ or }x=2 \\
\end{align}$
Since $x\le 0$, both x = 3 and x =2 are extraneous roots.
Hence the given equation has no real roots
Hence option D is correct.

Note: Alternative solution:
If we know the graph of f(x) then the graph of f(|x|) is the same as the graph f(x) for x>0 and for $x\le 0$ the graph is the mirror image taken in the y-axis.
Let $f(x)={{x}^{2}}+5x+6$
Then $f\left( \left| x \right| \right)={{x}^{2}}+5\left| x \right|+6$
First, we draw the graph of f(x)

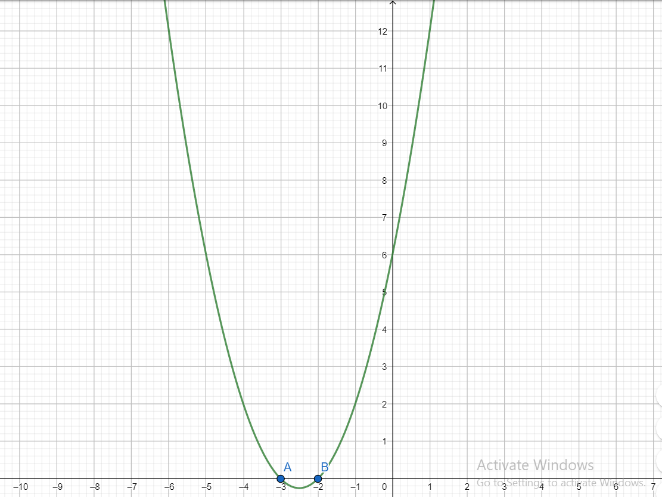
Then using the above-mentioned fact, we draw the graph of f(|x|)

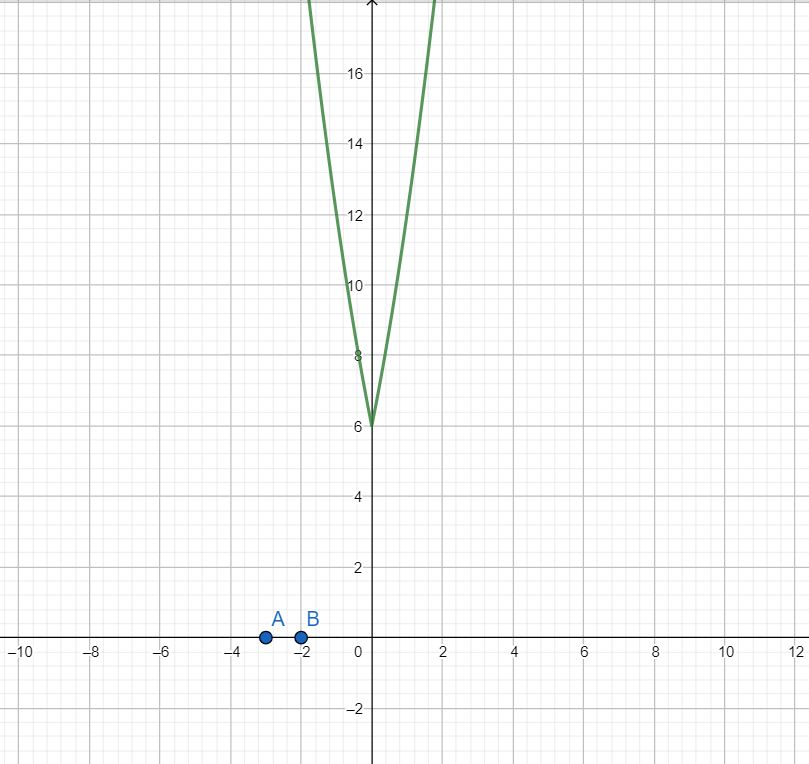
As is evident from the graph, the function f(|x|) does not have any root because it does not intersect the x-axis.
Hence the given equation ${{x}^{2}}+5\left| x \right|+6=0$ has no real roots.