Question

What will be the sum of all exterior angles of a polygon ?

Answer 1

Hint: For instance, let us draw any 4-sided polygon called square and then understand what will be exterior angles for a polygon.

As we know that reflex angles are the angles greater than \[{180^0}\].

Complete step-by-step answer:

Now as we know that every regular polygon has exterior angles. But these angles are not reflex angles.
As this is a misunderstanding that exterior angles are created by rotating from the exterior of one side to the next.
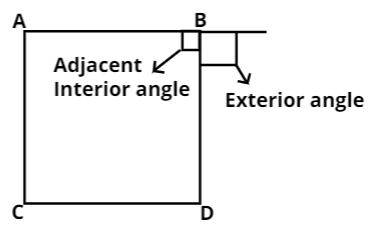
So, now for instance in a square the exterior angle is not \[{\text{36}}{{\text{0}}^{\text{0}}}{\text{ - 9}}{{\text{0}}^{\text{0}}}{\text{ = 27}}{{\text{0}}^{\text{0}}}\]. As if we were rotating from one side all the way around the vertex to the other side.
So, as we know that exterior angles are created by extending one side of the regular polygon past the shape, and then measuring the degrees from that extended line back to the next side of the polygon.
Since we are extending a side of the polygon, that exterior angle must necessarily be supplementary to the polygon’s interior angle. This means that together, the adjacent interior and exterior angles will add to \[{180^0}\].
So, for square exterior angle of any vertex will be \[{\text{18}}{{\text{0}}^{\text{0}}}{\text{ - 9}}{{\text{0}}^{\text{0}}}{\text{ = 9}}{{\text{0}}^{\text{0}}}\].
Now coming to the sum of exterior angles of the polygon having n sides.
As we know that, exterior angle + interior angle = \[{180^0}\].
So, if the polygon has n sides, then
Sum of all exterior angles + Sum of all interior angles = n * \[{180^0}\]
So, sum of all exterior angles = n * \[{180^0}\] - Sum of all interior angles
And as we know that any polygon has n sides. Its sum of all interior angles is equal to (n – 2) * \[{180^0}\].
So, sum of all exterior angles = n * \[{180^0}\] - (n – 2) * \[{180^0}\]
Now solving the above equation. We get,
So, sum of all exterior angles = n * \[{180^0}\] - n * \[{180^0}\] + 2 * \[{180^0}\] = \[{\text{36}}{{\text{0}}^{\text{0}}}\].
Hence, the sum of all exterior angles of a polygon is equal to \[{\text{36}}{{\text{0}}^{\text{0}}}\].

Note: Whenever we come up with this type of problem then first, we have to find the value of exterior for one vertex of the polygon and then we can multiply that by the number of sides of the polygon to get the sum of all exterior angles of the polygon.