Question

The speed v varies with time as \[\sqrt v = t\], the correct graph between $v$ and $t$ will be
A.

B.

C.

D.

Answer 1

Hint: In this question, the equation provided here, between the velocity of the body and the time interval, we will try to convert it in a way where the power of the velocity which is in the Y-axis equal to one. By doing this, we will then analyze the equation and find out which type of curve represents the equation.

Complete answer:
Here, the graphs are shown for the velocity on the Y-axis and the time for the X-axis for the graph. Velocity is a vector quantity. It is defined as the displacement of the particle when it travels per unit second of a time. The unit of velocity is \[m/s\]. In terms of formula, velocity is given as \[v = \dfrac{d}{t}\]. Here, v is the velocity, d is the displacement and t is the time taken by the body to travel a displacement d.

Here, in our case, the relationship between velocity and time is provided as \[\sqrt v = t\].Thus, to obtain a velocity time graph, we will have to make velocity, the subject of the formula. Hence, squaring both the sides of the above equation, we will obtain time in terms of velocity as shown below.
\[v = {t^2}\]
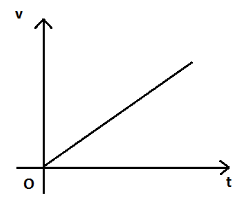
Above is an equation for a parabola curving towards the Y-axis.

Hence, option D is the correct answer.

Note: Here, for an equation of parabola, the parabola is always in two quadrants, for example, for the equation\[v = {t^2}\] the parabola for the equation lays in the first quadrant as well as the second quadrant. But the reason that the answer only lies in the first quadrant is because the negative value of the Y-axis is not allowed as there are no negative values in a square root.