
The solubility product of a sparingly soluble salt $AB$ at room temperature is $1.21\times {{10}^{-6}}$. Its molar solubility is:
(A) $1.21\times {{10}^{-6}}$
(B) $1.21\times {{10}^{-3}}$
(C) $1.1\times {{10}^{-4}}$
(D) $1.1\times {{10}^{-3}}$
Answer
362.7k+ views
Hint: When a salt is stirred in water and only a small amount of it gets dissolved but a large amount of it remains undissolved, then the salt is known as sparingly soluble salt. The solubility product of a sparingly soluble salt forming a saturated solution in water is calculated as the product of the concentrations of the ions, raised to a power equal to the number of the ions occurring in the equation representing the dissociation of the electrolyte. The solubility product is denoted by ${{K}_{sp}}$.
Formula Used: The formula for the solubility product depends on the number of ions formed after dissociation of the compound. For a sparingly soluble salt $AB$. The solubility product is given by ${{K}_{sp}}=\left[ {{A}^{+}} \right]\left[ {{B}^{-}} \right]$ where ${{A}^{+}}$ are the cations, ${{B}^{-}}$ are the anions.
Complete Step by Step Solution:
$AB$gets dissociated as
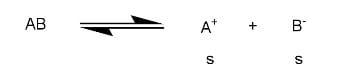
Let solubility be s
${{K}_{sp}}=\left[ {{A}^{+}} \right]\left[ {{B}^{-}} \right]$
${{K}_{sp}}=s\times s$
${{K}_{sp}}={{s}^{2}}$
The given solubility product is ${{K}_{sp}}=1.21\times {{10}^{-6}}$ .
${{s}^{2}}=1.21\times {{10}^{-6}}$
$s=\sqrt{1.21\times {{10}^{-6}}}$
$s=1.1\times {{10}^{-3}}$
Hence, the solubility of $AB$ is $1.1\times {{10}^{-3}}$ moles/litre.
Correct Option: (D) $1.1\times {{10}^{-3}}$
Note: The solubility product depends upon the temperature. It increases with an increase in temperature. This is because with an increase in temperature, solubility increases. Solubility means the tendency of a solute to get dissolved in a solvent to form a solution. The higher the value of a solubility product, the greater the solubility of the substance. It also depends on the common-ion effect; that is, if a common ion is present in the solution, then the solubility product gets lowered.
Formula Used: The formula for the solubility product depends on the number of ions formed after dissociation of the compound. For a sparingly soluble salt $AB$. The solubility product is given by ${{K}_{sp}}=\left[ {{A}^{+}} \right]\left[ {{B}^{-}} \right]$ where ${{A}^{+}}$ are the cations, ${{B}^{-}}$ are the anions.
Complete Step by Step Solution:
$AB$gets dissociated as
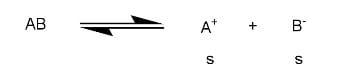
Let solubility be s
${{K}_{sp}}=\left[ {{A}^{+}} \right]\left[ {{B}^{-}} \right]$
${{K}_{sp}}=s\times s$
${{K}_{sp}}={{s}^{2}}$
The given solubility product is ${{K}_{sp}}=1.21\times {{10}^{-6}}$ .
${{s}^{2}}=1.21\times {{10}^{-6}}$
$s=\sqrt{1.21\times {{10}^{-6}}}$
$s=1.1\times {{10}^{-3}}$
Hence, the solubility of $AB$ is $1.1\times {{10}^{-3}}$ moles/litre.
Correct Option: (D) $1.1\times {{10}^{-3}}$
Note: The solubility product depends upon the temperature. It increases with an increase in temperature. This is because with an increase in temperature, solubility increases. Solubility means the tendency of a solute to get dissolved in a solvent to form a solution. The higher the value of a solubility product, the greater the solubility of the substance. It also depends on the common-ion effect; that is, if a common ion is present in the solution, then the solubility product gets lowered.
Recently Updated Pages
Questions & Answers - Ask your doubts

A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Two Planoconcave lenses 1 and 2 of glass of refractive class 12 physics CBSE

The compound 2 methyl 2 butene on reaction with NaIO4 class 12 chemistry CBSE

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Differentiate between an exothermic and an endothermic class 11 chemistry CBSE

Which places in India experience sunrise first and class 9 social science CBSE

The shortest day of the year in India

What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?




