Question

The shape of the interference fringes, on the screen, is

A. Circle
B. Ellipse
C. Parabola
D. Straight line

Answer 1

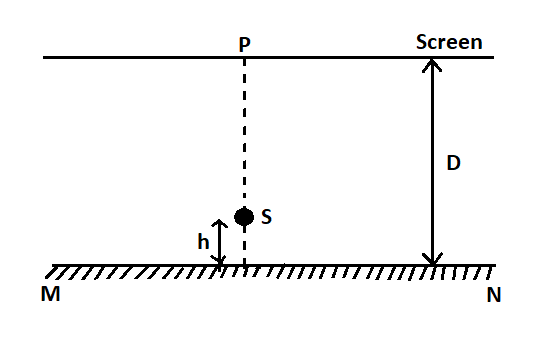
Hint: In the figure, we have a mirror $MN$. A point source $S$ due to the reflection of the mirror at a distance. We have a screen placed at a distance $D$. We have to find the shape of the interference fringes formed on the fringes. Interference happens when two rays from a coherent source interfere with each other. In such a case we will get a pattern of alternate bright and dark fringes.

Complete step by step answer:
We have the setup of the mirror and the object given in the figure.
We know that we need two rays for the formation of an interference pattern.
Therefore, let us consider another point source as shown in the figure below.

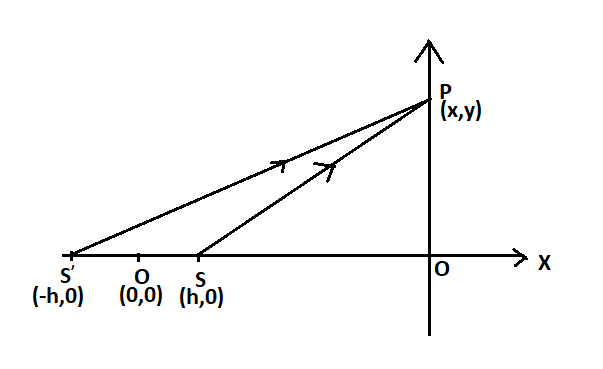
Let ${S'}$ be the other point source due to the reflection of the mirror.
The two rays $S$ and ${S'}$ are coherent and can produce an interference pattern.
Let us consider that the two rays meet at a point $P$ on the screen,
We can write the distance $SP$ as,
$SP = \sqrt {{{(x - h)}^2} + {y^2}} $ (using hypotenuse theorem)
We can write the distance ${S'}P$ as,
${S'}P = \sqrt {{{(x + h)}^2} + {y^2}} $
Let us take $\Delta $to be the path difference at the point $P$
The path difference can be written as,
$\Delta = {S'}P - SP$
From this we can write,
$\Delta + SP = {S'}P$
Squaring on both sides, we get
${\left( {\Delta + SP} \right)^2} = {\left( {{S'}P} \right)^2}$
Substituting the values of $SP$and ${S'}P$ we get
\[{\left( {\Delta + \sqrt {{{(x - h)}^2} + {y^2}} } \right)^2} = {\left( {\sqrt {{{\left( {x + h} \right)}^2} + {y^2}} } \right)^2}\]
On solving we get
${\Delta ^2} + \left( {{x^2} + {h^2} - 2hx} \right) + {y^2} + 2\Delta \sqrt {{{(x - h)}^2} + {y^2}} = \left( {{x^2} + {h^2} + 2xh} \right) + {y^2}$
Cancelling the common terms and rearranging the equation we get,
${\Delta ^2} - 4hx = - 2\Delta \sqrt {{{\left( {x - h} \right)}^2} + {y^2}} $
Again squaring the equation,
${\left( {{\Delta ^2} - 4hx} \right)^2} = {\left( { - 2\Delta \sqrt {{{\left( {x - h} \right)}^2} + {y^2}} } \right)^2}$
Squaring we get
${\Delta ^4} + 16{h^2}{x^2} - 8hx{\Delta ^2} = 4{\Delta ^2}({x^2} + {h^2} - 2hx) + {y^2}$
Expanding the equation we get,
${\Delta ^4} + 16{h^2}{x^2} - 8hx{\Delta ^2} = 4{\Delta ^2}{x^2} + 4{\Delta ^2}{h^2} - 8hx{\Delta ^2} + {y^2}$
Eliminating the common terms and rearranging the equation we get,
$16{h^2}{x^2} - 4{\Delta ^2}{x^2} + {y^2} = 4{\Delta ^2}{h^2} - {\Delta ^4}$
Making the LHS in terms of ${x^2}$and ${y^2}$we get
$\left( {16{h^2} - 4{\Delta ^2}} \right){x^2} + {y^2} = 4{h^2}{\Delta ^2} - {\Delta ^4}$
This equation is of the form, ${x^2} + {y^2} = {r^2}$
This is the equation for circle,
Hence fringes will appear circular.

So, the correct answer is “Option A”.

Note:
Light waves are considered electromagnetic waves. When two light waves of the same frequency overlap with each other interference happens and we get a pattern on the screen. The effect of the resultant pattern will depend on the amplitude of waves as well as the phases of the two waves. The resultant wave of interference is explained by the principle of superposition.