The shadow of a tower, when the angle of elevation of the sun is \[{45^0}\], is found to be 10 m longer than when it was \[{60^0}\]. Find the height of the tower.
Answer
Verified360.6k+ views
Hint: Shadow of any object is always perpendicular to the object itself. So, let us use this to find the height of the tower.
Complete step-by-step answer:
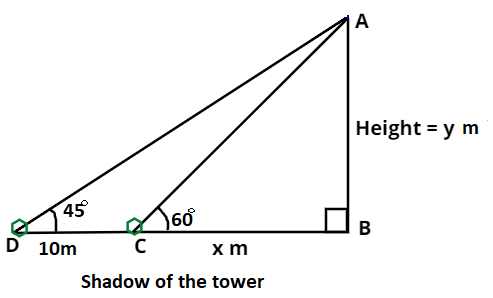
Above figure is drawn with respect to the given conditions in question.
As we can see from the above figure that,
Height of the tower is AB.
And length of shadow is 10m more when the angle of elevation is ${45^0}$ instead of \[{60^0}\]i.e.
So, let the length of shadow when the angle of elevation is \[{60^0}\] (\[\angle {\text{ACB}}\]) be x metres.
Then the length of shadow when the angle of elevation is ${45^0}$ (\[\angle {\text{ADB}}\]) be (x + 10) metres.
Let the height of the tower be (AB) y metres.
And the length of DC (see in figure) is 10 metres.
Here we are known with perpendicular and base of \[\Delta {\text{ABC}}\] and \[\Delta {\text{ABD}}\].
So, we will only use trigonometric functions, that include perpendicular and base.
So, as we know that, $\tan \theta = \dfrac{{Perpendicular}}{{Base}}$.
So, as we can see from the above figure that, ${\text{tan 4}}{{\text{5}}^{\text{0}}}{\text{ = }}\dfrac{{{\text{AB}}}}{{{\text{BD}}}}{\text{ = }}\dfrac{{\text{y}}}{{{\text{x + 10}}}}$.
And we know that \[{\text{tan 4}}{{\text{5}}^{\text{0}}}{\text{ = 1}}\].
So, x + 10 = y
And x = y – 10 …...(1)
And, ${\text{tan 6}}{{\text{0}}^{\text{0}}}$ = $\dfrac{{{\text{AB}}}}{{{\text{BC}}}}{\text{ = }}\dfrac{{\text{y}}}{{\text{x}}}$.
Now, putting the value of ${\text{tan 6}}{{\text{0}}^{\text{0}}}$ and x from equation 1. We get,
\[
\sqrt 3 {\text{ }} = {\text{ }}\dfrac{{\text{y}}}{{{\text{y }} - {\text{ }}10}} \\
\Rightarrow \left( {{\text{y }} - {\text{ }}10} \right)\sqrt 3 {\text{ }} = {\text{ y}} \\
\Rightarrow {\text{y }} = {\text{ }}\dfrac{{10\sqrt 3 }}{{\left( {\sqrt 3 {\text{ }} - {\text{ }}1} \right)}}{\text{ }} \approx {\text{ }}23.66{\text{ m}} \\
\]
Now, as we have defined above that the height of the tower is y metres.
Hence, the height of the tower will be 23.66 metres.
Note: Whenever you come up with this type of problem then first, we should draw a figure according to the given conditions in question. And then we will assume the height of the tower as y metres and then after using trigonometric functions like \[{\text{tan}}\theta \] we can get different equations. Then solve these equations to get the value of y. And at last we can approximate our answer up to two decimal places.
Complete step-by-step answer:
Above figure is drawn with respect to the given conditions in question.
As we can see from the above figure that,
Height of the tower is AB.
And length of shadow is 10m more when the angle of elevation is ${45^0}$ instead of \[{60^0}\]i.e.
So, let the length of shadow when the angle of elevation is \[{60^0}\] (\[\angle {\text{ACB}}\]) be x metres.
Then the length of shadow when the angle of elevation is ${45^0}$ (\[\angle {\text{ADB}}\]) be (x + 10) metres.
Let the height of the tower be (AB) y metres.
And the length of DC (see in figure) is 10 metres.
Here we are known with perpendicular and base of \[\Delta {\text{ABC}}\] and \[\Delta {\text{ABD}}\].
So, we will only use trigonometric functions, that include perpendicular and base.
So, as we know that, $\tan \theta = \dfrac{{Perpendicular}}{{Base}}$.
So, as we can see from the above figure that, ${\text{tan 4}}{{\text{5}}^{\text{0}}}{\text{ = }}\dfrac{{{\text{AB}}}}{{{\text{BD}}}}{\text{ = }}\dfrac{{\text{y}}}{{{\text{x + 10}}}}$.
And we know that \[{\text{tan 4}}{{\text{5}}^{\text{0}}}{\text{ = 1}}\].
So, x + 10 = y
And x = y – 10 …...(1)
And, ${\text{tan 6}}{{\text{0}}^{\text{0}}}$ = $\dfrac{{{\text{AB}}}}{{{\text{BC}}}}{\text{ = }}\dfrac{{\text{y}}}{{\text{x}}}$.
Now, putting the value of ${\text{tan 6}}{{\text{0}}^{\text{0}}}$ and x from equation 1. We get,
\[
\sqrt 3 {\text{ }} = {\text{ }}\dfrac{{\text{y}}}{{{\text{y }} - {\text{ }}10}} \\
\Rightarrow \left( {{\text{y }} - {\text{ }}10} \right)\sqrt 3 {\text{ }} = {\text{ y}} \\
\Rightarrow {\text{y }} = {\text{ }}\dfrac{{10\sqrt 3 }}{{\left( {\sqrt 3 {\text{ }} - {\text{ }}1} \right)}}{\text{ }} \approx {\text{ }}23.66{\text{ m}} \\
\]
Now, as we have defined above that the height of the tower is y metres.
Hence, the height of the tower will be 23.66 metres.
Note: Whenever you come up with this type of problem then first, we should draw a figure according to the given conditions in question. And then we will assume the height of the tower as y metres and then after using trigonometric functions like \[{\text{tan}}\theta \] we can get different equations. Then solve these equations to get the value of y. And at last we can approximate our answer up to two decimal places.
Last updated date: 23rd Sep 2023
•
Total views: 360.6k
•
Views today: 5.60k
