Question

The root system in a plant is well developed
(a)Due to the deficiency of auxin
(b)Due to the deficiency of cytokinins
(c)Due to the deficiency of minerals
(d)For the increased absorption of water

Answer 1

Hint: The root is the part of the plant that develops from the radicle of the seed. Roots are not seen in some plants like mosses and liverworts instead root-like structures known as rhizoids are seen in them which provide support, water, minerals.

Complete answer:
The root system in a plant is well developed for the increased absorption of water and minerals. This is because the roots are present inside the soil layer where most of the water and minerals are found. The root system has special modifications like root hair which are cellular extensions of the epidermal cells to increase the surface area for absorption. The root cells also actively absorb minerals against the concentration gradient in order to have a hypertonic protoplasm. This allows for the absorption of more water inside the root cells. Along with absorption, roots also provide support and anchorage to the plant, storage of food material as well as synthesis of phytohormones.

Additional Information: Let us learn more about the root system in plants.
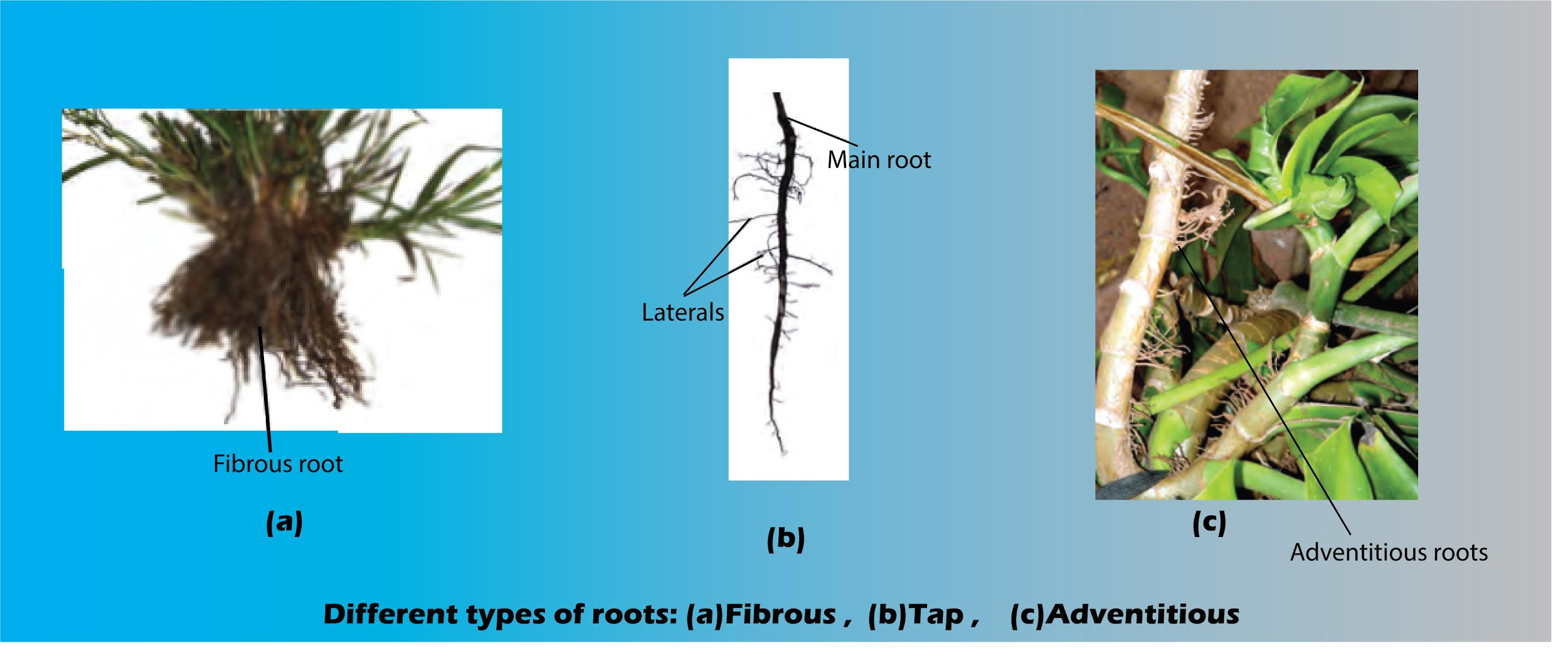
-Dicots have taproots in which the primary root is formed by the direct elongation of the radicle and many lateral roots such as secondary, tertiary, etc, grow from the primary root. Example-Mustard plant.
-Monocots have fibrous roots in which the primary root is short-lived and is replaced by a bunch of a large number of roots that arise from the base of the stem. Example-Wheat plant.
-There are also some plants in which roots arise from parts other than the radicle like the aerial roots of Banyan, they are known as adventitious roots.
-The aerial roots of the Banyan tree are known as prop roots and they arise out of the stem to provide support to the heavy lateral branches.
So, the correct option is ‘For the increased absorption of water’.

Note: -Plant hormones also known as phytohormones are responsible for the growth and regulation of the plant.
-The main plant growth regulators (PGRs) include auxin, cytokinin, gibberellin, abscisic acid, and ethylene.
-Auxin is responsible for the growth of plants towards the direction of the light source and includes compounds like indole-3-acetic acid.
-Cytokinin is responsible for cytokinesis and helps in the differentiation of cells along with auxin.