Question

The refractive index of the material of a prism is $\sqrt 2 $ and the angle of the prism is \[30^\circ \]. One of the two refracting surfaces of the prism is made a mirror inwards, by silver coating. A beam of monochromatic light entering the prism from the other face will retrace its path (after reflection from the silvered surface) if its angle of incidence on the prism is?
A. \[30^\circ \]
B. \[60^\circ \]
C. \[zero\]
D. \[45^\circ \]

Answer 1

Hint: Our first step will be to determine the refractive angle. After that, we will use snell’s law for the air-prism medium to determine the incident angle on the face of the prism.

Formula Used: Snells’ Law: $\dfrac{{{\mu _1}}}{{{\mu _2}}} = \dfrac{{\sin r}}{{\sin i}}$
Where \[{\mu _1},{\mu _2}\] are the refractive indices of medium one and medium two and $i,r$ are the angles of incidence from medium one to two and refraction from medium two to one.

Complete step by step answer:
According to the conditions given in the question, a monochromatic beam is to retrace its own path after entering the prism from air and reflecting on the mirrored surface of the prism.
The prism has a $30^\circ $ prism angle and a refractive index of $\sqrt 2 $. We are supposed to find the angle of incidence so that the ray retraces its path. We also know that the refractive index of air is $1$.
The phenomenon will look as below:

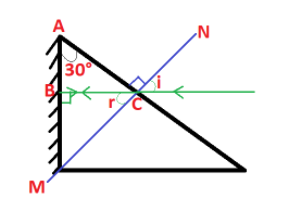
In triangle $ABC$, angle $A$ is $30^\circ $, $B$ is $90^\circ $. This is so because only a perpendicular incident ray will reflect off a mirror along its initial path. Therefore, angle $C$ is $180 - (30 + 90) = 60^\circ $.
$NM$ is the normal on the surface of the prism. Therefore it will cut the prism at $C$ normally. This means that the summation of angle $ACB$ and $BCM$ will be $90^\circ $.
Therefore, we get angle $BCM$ as $90 - 60 = 30^\circ $. That is $r = 30^\circ $.
Now applying Snells’ Law we get,
$
  \dfrac{{{\mu _1}}}{{{\mu _2}}} = \dfrac{{\sin r}}{{\sin i}} \\
   \Rightarrow \dfrac{1}{{\sqrt 2 }} = \dfrac{{\sin 30}}{{\sin i}} \\
   \Rightarrow i = {\sin ^{ - 1}}(\sqrt 2 \times \dfrac{1}{2}) = {\sin ^{ - 1}}\dfrac{1}{{\sqrt 2 }} \\
   \Rightarrow i = 45^\circ \\
 $
Therefore, a beam of monochromatic light entering the prism from the other face will retrace its path (after reflection from the silvered surface) if its angle of incidence on the prism is $45^\circ $.

In conclusion, the correct option is D.

Note:The conditions for retracing of a light beam must always be kept in mind. A mirror always reflects a light beam if it is incident on it normally. But if a bean is incident on a prism surface normally, it passes through it without refraction.