Question

The refractive index of glass is 1.5. Find the speed of light in glass, if its speed in air is $3\times {{10}^{8}}m{{s}^{-1}}$. Also find the critical angle for glass.

Answer 1

Hint: The given refractive index of glass is with respect to air. The refractive index of glass is given as the ratio of speed of light in vacuum to the speed of light in the medium. We can replace the speed of light in vacuum with the speed of light in air as they are approximately the same. The critical angle is the angle of incidence for which there is no refraction i.e. the angle of refraction is 90 degrees. Hence we can use Snell’s law to determine the critical angle.

Complete step-by-step answer:
Let us first define the refractive index of a medium in general and in terms of Snell’s law.
Refractive index of a medium is the ratio of the speed of the light in vacuum to its speed of light in the medium. This can be mathematically represented as,
$\eta =\dfrac{\text{Speed of light in (vacuum/air)}}{\text{Speed of light in medium}}...(1)$
According to Snell’s law, the refractive index of a medium is given by,
$\eta =\dfrac{\operatorname{sin}i}{\operatorname{sin}r}$ where I is the angle of incidence and r is the angle of refraction.
The refractive index of glass is given as 1.5 and speed of light in air is given as $3\times {{10}^{8}}m{{s}^{-1}}$.Hence we can use the equation 1 to determine the speed of light in the glass.
$\begin{align}
  & \eta =\dfrac{\text{Speed of light in (vacuum/air)}}{\text{Speed of light in medium}} \\
 & 1.5=\dfrac{3\times {{10}^{8}}}{\text{Speed of light in medium}} \\
 & \text{Speed of light in medium}=\dfrac{3\times {{10}^{8}}}{1.5}=2\times {{10}^{8}}m{{s}^{-1}}. \\
\end{align}$
Hence the speed of light in glass is $2\times {{10}^{8}}m{{s}^{-1}}$.

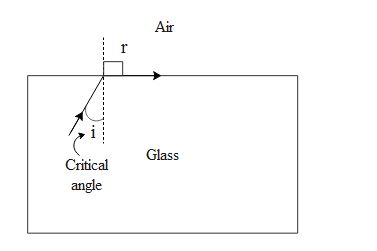
In the above diagram we can see that the refracted angle for angle of incidence or the critical angle is 90 degrees. Hence we can use Snell’s law to determine the critical angle of incidence.
$\begin{align}
  & \eta =\dfrac{\operatorname{sin}i}{\operatorname{sin}r},\text{refractive index of air with respect to glass is }\dfrac{1}{\text{1}\text{.5}}=0.66 \\
 & 0.66=\dfrac{\operatorname{sin}i}{\operatorname{sin}90}\text{, sin90=1 hence} \\
 & \operatorname{sin}i=0.66 \\
 & i={{\operatorname{sin}}^{-1}}0.66 \\
 & i={{41.29}^{\circ }} \\
\end{align}$
Hence the critical angle for glass is 41.29 degrees.

Note: The refractive index of the medium has no units. As light enters from a rarer to denser medium it bends towards the normal. Whereas if light enters from denser to rarer medium it bends away from the normal of incidence.