Question

The probability density plots of \[{\text{1s}}\] and ${\text{2s}}$ atomic orbitals are given in the figures. The density of dots in a region represents the probability density of finding electrons in the region on the basis of the above diagram, which of the following statements is incorrect?

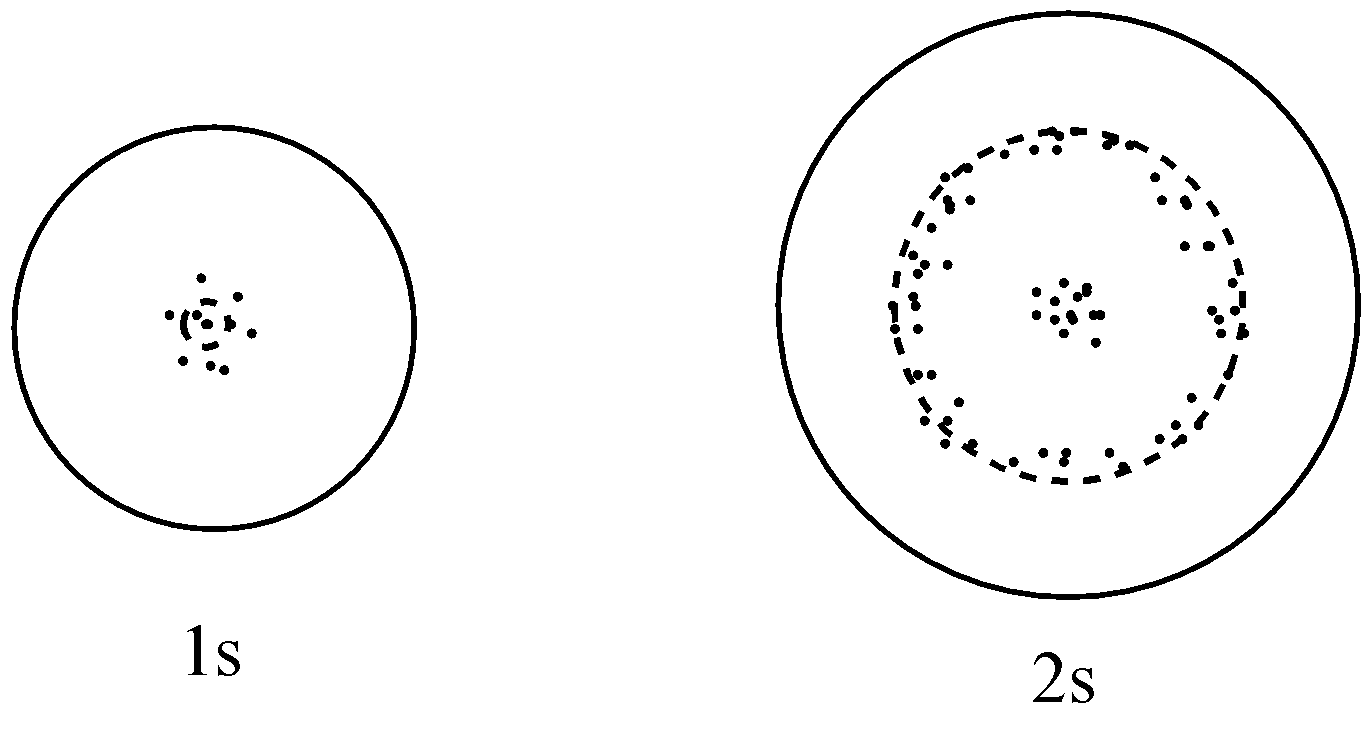
(a) \[{\text{1s}}\] and \[{\text{2s}}\] orbitals are spherical in shape
(b) The probability of finding the electron is maximum near the nucleus.
(c) The probability of finding the electron at a given distance is equal in all directions.
(d)  The probability density of electrons for \[{\text{2s}}\] orbital decreases uniformly as distance from the nucleus increases.

Answer 1

Hint: Probability density gives the probability of finding an electron in a given volume. Since, $s$ orbitals are spherical in shape, so, their probability density will depend only on the radius of the sphere.

Complete step by step answer:
For option (a), it is given that \[1s\] and $2s$ orbital are spherical in shape which is a true statement because it is known, and can be seen from the given figure.
For option (b), it is given that the probability of finding the electron is maximum near the nucleus which is a correct statement because it can be seen that the population of dots which represents the probability density is maximum near the nucleus. So, the probability of finding the electrons will be maximum there.
For option(c), it is given that the probability of finding the electron at a given distance is equal in all directions, and this statement is true only in the case of $s$ orbitals because they are spherical in shape and spherical surfaces have uniform distributions.
For option (d), it is given that the probability density for $2s$ orbital decreases uniformly as distance from the nucleus increases which is an incorrect statement because in $2s$ orbital, there is one node (where the probability of finding the electron is zero). So, the probability density here will increase first, and then decreases to minimum. So, it is no longer uniform as we move away from the nucleus.

So, the correct answer is Option C .

Note:
For finding the nodes (zero electron density), use the formula $\left( {n - 1} \right)$ where $n$ is the principal quantum number. The two types of nodes are angular node (given by the value of azimuthal quantum number $l$) and radial node (given by the formula $\left( {n - 1 - l} \right)$, $n$ is principal and $l$ is azimuthal quantum number).