Question

The parallel sides of a trapezium are 25 cm and 11cm, while its non-parallel sides are 15cm and 13cm. Find the area of the trapezium.

Answer 1

Hint:
We will first draw a line parallel to one side. Then, find the area of the formed triangle using Heron’s formula and equate it to the formula $\dfrac{1}{2} \times {\text{base}} \times {\text{height}}$ to find the height of the trapezium. Then, substitute the values in the formula, $\dfrac{1}{2}\left( {a + b} \right)h$, where $a,b$ are lengths of parallel sides of trapezium and $h$ is the height between the set of parallel lines of trapezium.

Complete step by step solution:
We are given that length of parallel sides of a trapezium is 25 cm and 11cm, while its non-parallel sides are 15cm and 13cm.
We will calculate the area of the trapezium.
We know that the area of the trapezium is $\dfrac{1}{2}\left( {a + b} \right)h$, where $a,b$ are lengths of parallel sides of trapezium and $h$ is the height between the set of parallel lines of trapezium.
We will first calculate the height of the trapezium.
Consider a trapezium $ABCD$
Draw a line $AP$ parallel to $BC$ and draw a perpendicular from $A$ on $DC$

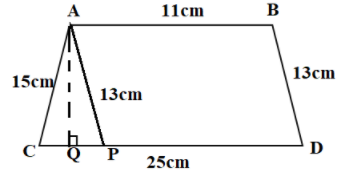
Now, length of $CP$ can be obtained by subtracting length of $PD$ which is equal to $AB$ from the length of $CD$
That is,
$CP = 25 - 11 = 14$cm
Now, we will calculate the area of triangle $ACP$ using heron’s formula and then will use the formula $\dfrac{1}{2} \times {\text{base}} \times {\text{height}}$ to find the height.
For heron’s formula, let us find the semi-perimeter of the triangle which is equal to the half the perimeter of the triangle.
That is, $s = \dfrac{{AP + CP + AC}}{2} = \dfrac{{13 + 14 + 15}}{2} = \dfrac{{42}}{2} = 21cm$
Then, the area of the triangle is calculated using the formula, $\sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $, where $a,b,c$ are the sides of triangle.
$
  A = \sqrt {21\left( {21 - 13} \right)\left( {21 - 14} \right)\left( {21 - 15} \right)} \\
   \Rightarrow A = \sqrt {21\left( 8 \right)\left( 7 \right)\left( 6 \right)} \\
   \Rightarrow A = \sqrt {7 \times 3 \times 2 \times 4 \times 7 \times 2 \times 3} \\
   \Rightarrow A = 84c{m^2} \\
$
Also, the area of triangle is $\dfrac{1}{2} \times {\text{base}} \times {\text{height}}$
Therefore, $84 = \dfrac{1}{2} \times CP \times AQ$
On substituting the value of $CP$, we will get $AQ$ as,
$
  84 = \dfrac{1}{2} \times \left( {14} \right) \times AQ \\
   \Rightarrow AQ = 12cm \\
$
The area of the parallelogram is $\dfrac{1}{2}\left( {a + b} \right)h$, where $a,b$ are lengths of parallel sides of trapezium and $h$ is the height between the set of parallel lines of trapezium.
This implies the area of a parallelogram is
$
  A = \dfrac{1}{2}\left( {11 + 25} \right)\left( {12} \right) \\
  A = 36\left( 6 \right) \\
   = 216c{m^2} \\
$

Thus, the area of the trapezium is $216c{m^2}$

Note:
A trapezium is a quadrilateral with a set of parallel lines and a set of non-parallel lines. Here, we calculated the area of trapezium by using the formula is $\dfrac{1}{2}\left( {a + b} \right)h$, where $a,b$ are lengths of parallel sides of trapezium and $h$ is the height but we can also add the area of triangle which we calculated in above steps to the area of parallelogram, which is ${\text{base}} \times {\text{height}}$.