Question

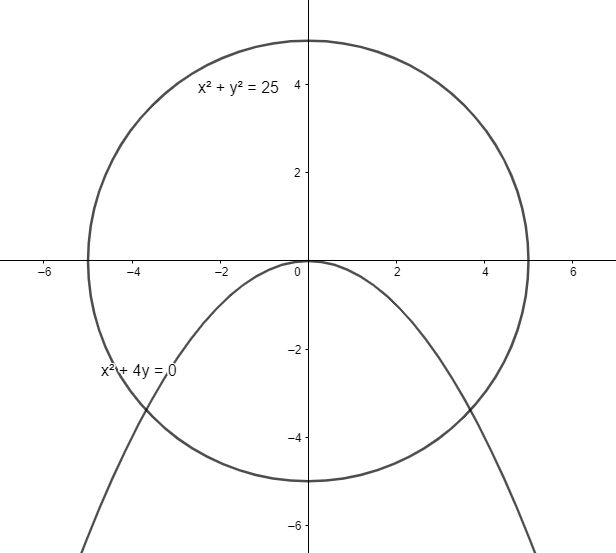
The number of points with integral coordinates \[(2a,a-1)\]that fall in the interior
 of the larger segment of the circle \[{{x}^{2}}+{{y}^{2}}=25\] cut off by the parabola
 x\[{{x}^{2}}+4y=0\]is
(a) One
(b) Two
(c) Three
(d) None of these

Answer 1

Hint: We will substitute the coordinates of points in the equation of both curves
 and check if the value is positive or negative.

We have a circle\[{{x}^{2}}+{{y}^{2}}=25\] and a parabola\[{{x}^{2}}+4y=0\].
We want to find the points with integral coordinates that fall in the interior of the larger
segment of the circle cut off by the parabola.
To find the points which lie in the larger segment of the circle \[{{x}^{2}}+{{y}^{2}}=25\]cut off
 by the parabola\[{{x}^{2}}+4y=0\], we will substitute the points in the equation of the circle
and the parabola.

Substituting the point \[(2a,a-1)\]in the equation of parabola\[{{x}^{2}}+4y=0\], we will get
positive value as the above equation has no real roots.
Substituting the values, we get
\[\begin{align}
  & \Rightarrow {{(2a)}^{2}}+4(a-1)>0 \\
 & \Rightarrow 4{{a}^{2}}+4a-4>0 \\
 & \Rightarrow {{a}^{2}}+a-1>0 \\
\end{align}\]
We observe that this holds true for all\[a>1\].
While, substituting the point \[(2a,a-1)\]in the equation of circle\[{{x}^{2}}+{{y}^{2}}=25\], we
 will get a negative value.
Substituting the values, we get
\[\begin{align}
  & \Rightarrow {{(2a)}^{2}}+{{(a-1)}^{2}}-25<0 \\
 & \Rightarrow 5{{a}^{2}}-2a-24<0 \\
\end{align}\]
We will now factorize the above equation.
\[\begin{align}
  & \Rightarrow 5{{a}^{2}}+10a-12a-24<0 \\
 & \Rightarrow 5a(a+2)-12(a+2)<0 \\
\end{align}\]
So, we have \[(a+2)(5a-12)<0\]
If\[a+2>0,5a-12<0\], the possible values of\[a\]are {-1, 0, 1, 2}.
If\[a+2<0,5a-12>0\], no such value of \[a\]exists.
As 4 different values of \[a\]exist, we have 4 different points that lie in the larger segment of
 the circle bounded by the parabola.
Hence, the correct answer is None of these
 Note: It is very necessary to keep in mind that we want to find the points lying in the larger
 section of the circle bounded by the parabola and not the smaller segment. if we solve the
 question for the smaller segment, we will get equations with opposite inequalities and thus,
we will get a wrong answer.