Question

The mean and S.D of marks obtained by 50 students of a class in three subjects, mathematics, physics, and chemistry are given below: 

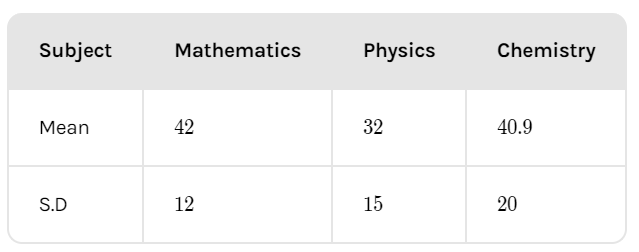
Which of the three subjects shows the lowest coefficient of variation?

Answer 1

Hint: The coefficient of variation is given by the formula \[C.V=\dfrac{S.D}{mean}\times 100\], here S.D is the standard deviation and the mean is the average of all the data. C.V is the coefficient of variation of the data set whose mean and standard deviation is given for different subjects.

Complete step-by-step answer:
In the question, it is given that the mean and S.D of marks obtained by 50 students of a class in three subjects, mathematics, physics, and chemistry are as follows:

Now, we have to find the subject with the lowest coefficient of variation. So here we know that the higher the coefficient of variation, more is the deviation from the mean of the data. The standard deviation is the measure that gives the percentage of data that lies around the mean. Also, we know that the mean is the average of the data given.
Now the formula that we use to find the coefficient of variation is given as: \[C.V=\dfrac{S.D}{mean}\times 100\].
Here, S.D is the standard deviation and the mean is the average of all the data. Also, C.V is the coefficient of variation. So, we will find the coefficient of variation of each subject as shown below:
Coefficient of variation for Mathematics is:
\[\begin{align}
  & \Rightarrow C.V=\dfrac{S.D}{mean}\times 100 \\
 & \Rightarrow C.V=\dfrac{12}{42}\times 100 \\
 & \Rightarrow C.V=28.57 \\
\end{align}\]
Similarly, Coefficient of variation for Physics is:
\[\begin{align}
  & \Rightarrow C.V=\dfrac{S.D}{mean}\times 100 \\
 & \Rightarrow C.V=\dfrac{15}{32}\times 100 \\
 & \Rightarrow C.V=46.875 \\
\end{align}\]
Similarly, Coefficient of variation for Chemistry is:
\[\begin{align}
  & \Rightarrow C.V=\dfrac{S.D}{mean}\times 100 \\
 & \Rightarrow C.V=\dfrac{20}{40.9}\times 100 \\
 & \Rightarrow C.V=48.89 \\
\end{align}\]
So now, we can see that Mathematics shows the lowest coefficient of variation, i.e, \[C.V=28.57\].

Note: It can be noted that the coefficient of variation is very different from the variance. The variance is the squared of standard deviation, S.D. Also, be careful to multiply the ratio \[\dfrac{S.D}{mean}\] by 100 when we are finding the coefficient of variation.