Question

The magnitude of resultant of three vectors of magnitude 1, 2 and 3 whose direction are those of the sides of an equilateral triangle taken in order is:
A. $0$
B. $2\sqrt 2 $ units
C. $4\sqrt 3 $ units
D. $\sqrt 3 $ units

Answer 1

Hint: First, simplified and shift the vectors by connecting the tails of each vector and then break the vectors in the rectangular components in the form of $\hat i$ and $\hat j$ finally obtain the vectors sum of the vectors and the magnitude of the sum.

Complete step by step answer:
From the question, we know that the magnitude of the three vectors are $\vec A = 1,\;\vec B = 2$ and $\vec C = 3$ and these three vectors forms an equilateral triangle.We know that the all the angles of the equilateral triangle is equal to $60^\circ $ and the figure below represents the three vectors and the simplified representation of these three vectors.

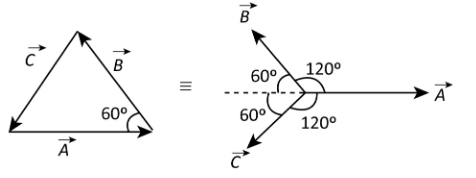
Now write the all vectors in terms of direction $\hat i$ and $\hat j$.
From the figure, we know that the vectors $\vec B$ and $\vec C$ are at angle $60^\circ $ so we will split them into the rectangular components.The vector $\vec A$ is written as,
$\vec A = 1\hat i$
The vector $\vec B$ is written as,
$\vec B = - \vec B\cos 60^\circ \hat i + \vec B\sin 60^\circ \hat j$
Substitute the values in the above equation, we get,
$\vec B = - \left( 2 \right)\dfrac{1}{2}\hat i + \left( 2 \right)\dfrac{{\sqrt 3 }}{2}\hat j\\
\Rightarrow\vec B = - 1\hat i + \sqrt 3 \hat j
$
The vector $\vec C$ is written as,
$\vec C = - \vec C\cos 60^\circ \hat i - \vec C\sin 60^\circ \hat j$
Substitute the values in the above equation, we get,
$
\vec C = - \left( 3 \right)\dfrac{1}{2}\hat i - \left( 3 \right)\dfrac{{\sqrt 3 }}{2}\hat j\\
\Rightarrow\vec C = - \dfrac{3}{2}\hat i - \dfrac{{3\sqrt 3 }}{2}\hat j
$
Now we calculate the sum of the three vectors, we have,
$
\vec A + \vec B + \vec C = \left( {1\hat i} \right) + \left( { - 1\hat i + \sqrt 3 \hat j} \right) + \left( { - \dfrac{3}{2}\hat i - \dfrac{{3\sqrt 3 }}{2}\hat j} \right)\\
\Rightarrow\vec A + \vec B + \vec C = - \dfrac{3}{2}\hat i - \dfrac{{3\sqrt 3 }}{2}\hat j
$
Now, we calculate the magnitude of the three vectors,
$\left| {\vec A + \vec B + \vec C} \right| = \left| { - \dfrac{3}{2}\hat i - \dfrac{{3\sqrt 3 }}{2}\hat j} \right|$
After simplifying the above equation, we have,
\[
\left| {\vec A + \vec B + \vec C} \right| = \sqrt {{{\left( { - \dfrac{3}{2}} \right)}^2} + {{\left( { - \dfrac{{3\sqrt 3 }}{2}} \right)}^2}} \\
\Rightarrow\left| {\vec A + \vec B + \vec C} \right|= \sqrt {\dfrac{9}{4} + \dfrac{3}{4}} \\
\therefore\left| {\vec A + \vec B + \vec C} \right|= \sqrt {\dfrac{{12}}{4}}
\]
After simplifying the above equation, we get $\sqrt 3 $.

Thus, the magnitude of the resultant of three vectors of magnitude 1, 2 and 3 is $\sqrt 3 $ and option D is correct.

Note:Make sure the triangles are formed by connecting the head of one vector with the tail of another vector and while splitting the vectors in the rectangular components, make sure you add minus in for leftwards and downward direction. Only $\hat i$ quantity will add with $\hat i$ quantity not $\hat j$ quantity.