Question

The line \[\dfrac{x}{a}+\dfrac{y}{b}=1\] meets the axis of x and y at A and B respectively and the line \[y=x\] at C so that area of the triangle AOC is twice the area of the triangle BOC, O being the origin, then one of the position of C is:
(a) \[\left( a,a \right)\]
(b) \[\left( \dfrac{2a}{3},\dfrac{2a}{3} \right)\]
(c) \[\left( \dfrac{b}{3},\dfrac{b}{3} \right)\]
(d) \[\left( \dfrac{2b}{3},\dfrac{2b}{3} \right)\]

Answer 1

Hint: Find the coordinates where the line \[\dfrac{x}{a}+\dfrac{y}{b}=1\] meets the coordinate axis. Draw a suitable diagram with these points and apply the area condition mentioned in the question. Area of a triangle can be found using \[\dfrac{1}{2}\times base\times height\].

Given that the line \[\dfrac{x}{a}+\dfrac{y}{b}=1\]meets the x axis at A and y axis at B.
Now, for point A:
Let us put \[y=0\], in the line \[\dfrac{x}{a}+\dfrac{y}{b}=1\]
\[\dfrac{x}{a}+\dfrac{0}{b}=1\]
\[x=a\]
So, Point A is \[\left( a,0 \right)\].
For point B:
Let us put \[x=0\]in the line \[\dfrac{x}{a}+\dfrac{y}{b}=1\]
\[\dfrac{0}{a}+\dfrac{y}{b}=1\]
\[y=b\]
So, Point B is \[\left( 0,b \right)\].
Therefore, we can plot the below diagram with the data we obtained.

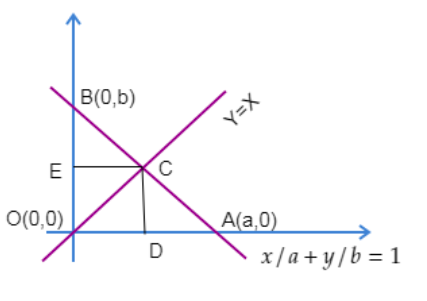
Now let us assume point C as \[\left( m,m \right)\]since it lies on the line \[x=y\].
As mentioned in the question we have:
(Area of \[\vartriangle AOC\]) = 2(Area of \[\vartriangle BOC\])
\[\dfrac{1}{2}\times \left( OA \right)\left( CD \right)=2\times \dfrac{1}{2}\left( OB \right)\left( CE \right)\]
Since, area of triangle = \[\dfrac{1}{2}\times base\times height\].
We have:
\[OA=a\]
\[CD=m\]
\[OB=b\]
\[CE=m\]
Substituting the above values in \[\dfrac{1}{2}\left( a \right)\left( m \right)=\left( b \right)\left( m \right)\], we will have:
\[\therefore \dfrac{1}{2}\left( a \right)\left( m \right)=\left( b \right)\left( m \right)\]
\[a=2b\]
Now let us substitute \[a=2b\] in the line \[\dfrac{x}{a}+\dfrac{y}{b}=1\]
\[\dfrac{x}{2a}+\dfrac{y}{b}=1...........(1)\]
Substituting \[c\left( m,m \right)\] in the equation (1), we will have:
\[\dfrac{m}{2b}+\dfrac{m}{b}=1\]
\[3m=2b\]
\[m=\dfrac{2b}{3}\]
Therefore, the coordinates of C can be \[\left( \dfrac{2b}{3},\dfrac{2b}{3} \right)\].
Hence option D is the correct answer.

Note: We can also find the are of the triangle using the formula \[\dfrac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right|\] when the three vertices of the triangle are known to us . But we adopt the formula of \[\dfrac{1}{2}\times base\times height\] to save time.