Question

The line $2x-y+1=0$ is tangent to the circle at the point $\left( 2,5 \right)$ and the centre of the circle lies on $x-2y=4$ . Then find the radius of the circle.

Answer 1

Hint: Sketch the diagram first to visualize the question better, then you could arrive at the answer merely by finding the perpendicular distance between the two lines.

Let’s sketch the situation given to us in the question. So we have a circle that has the line
$2x-y+1=0$ acting as a tangent to it at the point $(2,5)$, and we have the centre of the circle lying on the line $x-2y=4$. Drawing the figure while keeping all these features in mind, the diagram we’ll get is:

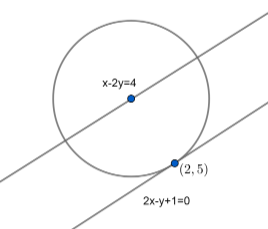
The lines do look parallel in the diagram, but from the equations of the lines, we can clearly see that they are not parallel.
Let’s assume the $y$ coordinate of the centre of the circle to be $=t$. Since we’re talking about the centre, the point will definitely satisfy the equation $x-2y=4$. Thus, we can find the $x$ coordinate of the centre simply by substituting for $y=t$ in the equation of the line. Doing so, we get :
$\begin{align}
  & x-2y=4 \\
 & \Rightarrow x=4+2y \\
 & \Rightarrow x=4+2\left( t \right)=4+2t \\
\end{align}$
So, the coordinates of the centre are :
$\therefore c\equiv \left( 4+2t,t \right)$
Now, let’s find out the distance between the centre and the tangent line. That will be found out by applying the formula using which we can find the perpendicular distance of any point $(X,Y)$ from the line $Ax+By+C=0$. So, if we assume the perpendicular distance of point $(X,Y)$ from the line $Ax+By+C=0$ is $d$, then : $d=|\dfrac{AX+BY+C}{\sqrt{{{A}^{2}}+{{B}^{2}}}}|$
Thus, here our point $(X,Y)=(4+2t,t)$ and our line $Ax+By+C=0$ is equal to the line $2x-y+1=0$.
Therefore, the perpendicular distance $d$ of point $(4+2t,t)$ from line $2x-y+1=0$ is :
\[\begin{align}
  & d=\left| \dfrac{AX+BY+C}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right| \\
 & \Rightarrow d=\left| \dfrac{2\left( 4+2t \right)-\left( t \right)+1}{\sqrt{{{\left( 2 \right)}^{2}}+{{\left( 1 \right)}^{2}}}} \right| \\
 & \Rightarrow d=\left| \dfrac{8+4t-t+1}{\sqrt{{{\left( 2 \right)}^{2}}+{{\left( 1 \right)}^{2}}}} \right| \\
 & \Rightarrow d=\left| \dfrac{\left( 3t+9 \right)}{\sqrt{5}} \right|...............(1) \\
\end{align}\]
And since, from the figure, we can see that this distance will also be equal to the radius of the circle,
$d=r=|\dfrac{3t+9}{\sqrt{5}}|$
Now, since the tangent touches the circle at the point $(2,5)$, the distance of the centre from this point will also be equal to the radius. So, by distance formula $\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}}$, we get :
\[\begin{align}
  & r=\sqrt{{{\left( (4+2t)-2 \right)}^{2}}+{{\left( t-5 \right)}^{2}}} \\
 & r=\sqrt{{{\left( 2+2t \right)}^{2}}+{{\left( t-5 \right)}^{2}}}............(\text{2)} \\
\end{align}\]
 By equating $(1)$ and $(2)$ with each other, we get;
$|\dfrac{\left( 3t+9 \right)}{\sqrt{5}}|=\sqrt{{{\left( 2+2t \right)}^{2}}+{{\left( t-5 \right)}^{2}}}$
Squaring both sides, we get :
$\begin{align}
  & \Rightarrow \dfrac{9{{t}^{2}}+81+54t}{5}={{(2+2t)}^{2}}+{{(t-5)}^{2}} \\
 & \Rightarrow 9{{t}^{2}}+81+54t=5[4+4{{t}^{2}}+8t+{{t}^{2}}+25-10t] \\
\end{align}$
$\begin{align}
  & \Rightarrow 9{{t}^{2}}-54t+81=5\left( 5{{t}^{2}}-2t+29 \right) \\
 & \Rightarrow 16{{t}^{2}}-64t+64=0 \\
\end{align}$
Dividing by $16$ on both sides, we get :
$\Rightarrow {{t}^{2}}-4t+4=0$



By factorising , we get :
$\begin{align}
  & {{\left( t-2 \right)}^{2}}=0 \\
 & \therefore t-2=0 \\
 & \\
\end{align}$
and the centre’s coordinates become :
$\begin{align}
  & C\left( 4+2t,t \right) \\
 & C\left( 4+\left( 2\times 2 \right),2 \right) \\
 & \therefore \\
\end{align}$
Now the radius will become;
$r=\sqrt{5{{\left( 2 \right)}^{2}}-\left( 2 \right)\times \left( 2 \right)+29}$
\[\therefore r=\sqrt{45}=3\sqrt{5}\] units.
Therefore, the radius of the circle is $3\sqrt{5}$ units.
Note: Most of the student make mistake in remembering formulae of distance i.e. $d=\left| \dfrac{AX+BY+C}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right|$ and finding radius, avoid calculation mistakes.