Question

The length of the chord joining the points $\left( 4\cos \theta ,4\sin \theta \right)$ and $\left[ 4\cos \left( \theta +{{60}^{\circ }} \right),4\sin \left( \theta +{{60}^{\circ }} \right) \right]$ of the circle ${{x}^{2}}+{{y}^{2}}=16$ is:
A. 4
B. 6
C. 2
D. 8

Answer 1

Hint: A chord is a line segment whose endpoints lie on the path of the circle. The given coordinates are in a parametric form of a circle and the angle suspended at the center is equal to ${{60}^{\circ }}$. From the equation of the circle, we can find out the radius of the circle. Then we have to solve the vertical component of the radius to find out the chord length.

Complete step by step solution:
The given endpoints of the chord are $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 4\cos \theta ,4\sin \theta \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)=\left[ 4\cos \left( \theta +{{60}^{\circ }} \right),4\sin \left( \theta +{{60}^{\circ }} \right) \right]$.
These are in a parametric form with respect to the center of the circle. By comparing the points, we can say that the angle suspended between these points is equal to ${{60}^{\circ }}$.
Let the length of the chord be assumed as L.

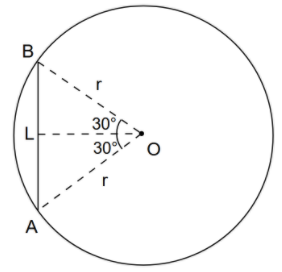
From the figure, we can see that $\dfrac{L}{2}=r\sin {{30}^{\circ }}$. Because $\dfrac{L}{2}$ is the opposite side and r is the hypotenuse side of the angle ${{30}^{\circ }}$.
Hence the length of the chord is given by the equation.
$\Rightarrow L=2r\sin {{30}^{\circ }}$ ……(1)
The standard form of the equation of the circle is ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$. By comparing this with the equation of the given circle, we can see that ${{r}^{2}}=16$.
$\Rightarrow r=4$
Let us now substitute our data in equation (1) to find out the length of the chord.
$\Rightarrow L=2\times 4\sin {{30}^{\circ }}=\dfrac{2\times 4}{2}$
$\Rightarrow L=4$

Hence the length of the chord is equal to 4 (Option A).

Note:
We can find out the length of the chord by using the property of an equilateral triangle. Consider the triangle AOB. We know that the sum of the internal angles of a triangle is 180 deg. Here we have one internal angle ${{60}^{\circ }}$. Since the two of the sides are equal, the remaining two angles must be equal to each other.
Assume that one of the unknown angles is x.
$\Rightarrow {{180}^{\circ }}-{{60}^{\circ }}={{120}^{\circ }}=2x$
$\Rightarrow x={{60}^{\circ }}$
All the three angles are equal and so it is an equilateral triangle. Hence the length of the chord is equal to the radius of the circle.