Question

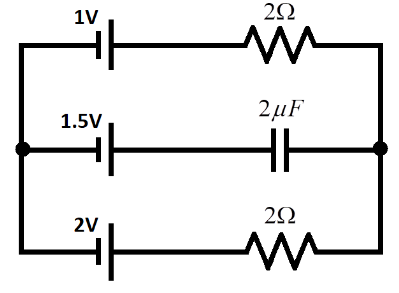
The charge in the $2\mu F$ capacitor at steady state is

A. Zero
B. $2\mu F$
C. $4\mu F$
D. $6\mu F$

Answer 1

Hint:In order to answer the above question, we will first of all discuss a capacitor and its steady state. Secondly, we will observe the circuit and draw the resultant circuit for a steady capacitor. Finally using Kirchhoff’s law, we will derive the voltage across the capacitor and the charge stored on the capacitor.

Formula used:
Kirchhoff’s Loop Rule: $\sum{V=0}$
Where $V$ is voltage.
Capacitance of a capacitor: $C=\dfrac{Q}{V}$
Where $C$ is the capacitance, $Q$ is the charge and $V$ is the voltage across the capacitor.

Complete step by step answer:
A capacitor is a two-terminal electrical component that can store energy in the form of an electric field. It is made up of two electrical conductors separated by a certain distance. The gap between the conductors can be filled with vacuum or a dielectric, which is an insulating material. Capacitance refers to the capacitor's capacity to store charges.

Capacitors store energy by separating opposing charge pairs. A parallel plate capacitor is the most basic design, consisting of two metal plates separated by a gap. However, capacitors come in a variety of shapes, sizes, heights, and girths, as well as a variety of materials.

When a capacitor is attached to a circuit, it starts charging. After the capacitor has fully charged, the current flowing through the capacitor will stop. Hence, when there is no current flowing through it, the capacitor will behave as an open circuit and it is said to be in steady state.

Now, if we look at the question, the capacitor having a capacity of $2\mu F$is said to be a steady capacitor. Therefore, the above circuit can be shown as

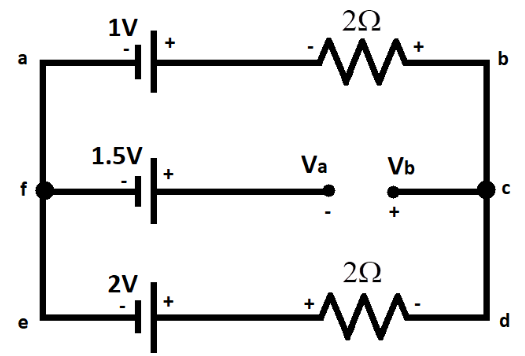
Here, the capacitor behaves as an open in the circuit. Now, if we consider the loop $edbae$ and apply Kirchhoff’s law, we get
$2-2I-2I-1=0 \\
\Rightarrow 4I=1 \\
\Rightarrow I=\dfrac{1}{4}=0.25A \\
\Rightarrow I=0.25A \\ $
Now, we know that the potential across the capacitor is shown by ${{V}_{a}}$ and ${{V}_{b}}$. Therefore, the potential difference across the capacitor is given as
${{V}_{c}}={{V}_{b}}-{{V}_{a}}$
Considering the loop $edcfe$ and using the Kirchhoff’s law, we get
$2-2I+{{V}_{b}}-{{V}_{a}}-1.5=0 \\
\Rightarrow {{V}_{b}}-{{V}_{a}}=1.5-2+2I \\ $
Using the result from above calculation $I=0.25A$ and taking ${{V}_{c}}={{V}_{b}}-{{V}_{a}}$, we get
${{V}_{c}}=1.5-2+2(0.25) \\
\Rightarrow {{V}_{c}}=-0.5+0.5 \\
\Rightarrow {{V}_{c}}=0 $
Thus, it can be said that the potential difference across the capacitor is zero.

As we know that the capacitance of the capacitor is given by the equation
$C=\dfrac{Q}{{{V}_{c}}}$
$\Rightarrow Q={{V}_{c}}\times C$
The capacitance of the capacitor is given as $2\mu F$ in the question. Thus, placing the values of $C$and ${{V}_{c}}$, we get
$Q=(0)2\times {{10}^{-6}} \\
\therefore Q=0 $
According to the equation above, it is proved that the charge stored on the capacitor is also zero as the potential difference across the capacitor is zero.

Hence, the correct answer is option A.

Note:It is very important to note that the capacitor can only be in a steady state when no amount of current is flowing through it. The first case is when the capacitor is fully charged. But we can see from our answer that the charge on the capacitor is zero. Hence, the capacitor hasn't charged at all. What does this mean? It means that in the above circuit, the capacitor faces the same potential difference which is opposite to each other on both the plates and it cancels out each other. i.e.
The voltage due to $2V$ battery in addition to the $2\Omega $ resistor = - (the voltage due to the $1.5V$ battery)
Therefore, the capacitor becomes neutral and no current flows through it and it remains discharged.