Question

The hypotenuse of a right-angled triangle is $ 17\;{\rm{cm}} $ and the difference between the other two sides is $ {\rm{7}}\;{\rm{cm}} $ . Find the other two unknown sides.

Answer 1

Hint: Since hypotenuse of the triangle is given, we will use the Pythagoras theorem to find the other two sides. We will also use the relation between the other two sides given in the question. Then we will use the formula for finding the roots of the quadratic equation. We will get one side from solving the expression. We will use this value to find the other side.

Complete step-by-step answer:
 We will draw a triangle $ \Delta ABC $ whose hypotenuse is $ {\rm{17}}\;{\rm{cm}} $ .

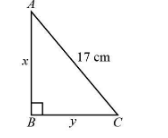
We will assume the base of the triangle $ BC $ as $ y\;{\rm{cm}} $ and the perpendicular of the triangle $ AB $ as $ x\;{\rm{cm}} $ .
 Since it is given on the question that the difference between the other two sides that is base and perpendicular is $ {\rm{7}}\;{\rm{cm}} $ . We can express it as:
 $ x\;{\rm{cm}} - y\;{\rm{cm}} = 7\;{\rm{cm}} $ ……(i)
Now, we will use Pythagoras theorem to express the relation between hypotenuse, perpendicular and base of the triangle which can be expressed as:
 $ {H^2} = {P^2} + {B^2} $
 In our triangle $ AB $ is the perpendicular, $ BC $ is the base and $ AC $ is the hypotenuse.
We will substitute $ x\;{\rm{cm}} $ for $ P $ , $ y\;{\rm{cm}} $ for $ B $ and $ {\rm{17}}\;{\rm{cm}} $ for $ H $ in the above expression.
 $ {\left( {{\rm{17}}\;{\rm{cm}}} \right)^2} = {\left( {x\;cm} \right)^2} + {\left( {y\;cm} \right)^2} $ ……(ii)
From equation (i) we have $ x\;{\rm{cm}} - y\;{\rm{cm}} = 7\;{\rm{cm}} $ which can be rewritten as:
\[x\;{\rm{cm}} = 7\;{\rm{cm + }}y\;{\rm{cm}}\] ……(iii)
We will substitute \[\left( {{\rm{7}}\;{\rm{cm + }}y\;{\rm{cm}}} \right)\] for \[x\;{\rm{cm}}\] in the equation (ii).
 $ {\left( {{\rm{17}}\;{\rm{cm}}} \right)^2} = {\left( {7\;{\rm{cm}} + y\;{\rm{cm}}} \right)^2} + {\left( {y\;{\rm{cm}}} \right)^2} $
Now, we will expand the above expression by using algebraic identity $ \left( {a + b} \right) = {a^2} + {b^2} + 2ab $ .
 $ \begin{array}{c}
{\left( {{\rm{17}}\;{\rm{cm}}} \right)^2} = {\left( {7\;{\rm{cm}}} \right)^2} + {\left( {y\;{\rm{cm}}} \right)^2} + 2\left( {7\;{\rm{cm}} \times {\rm{y}}\;{\rm{cm}}} \right) + {\left( {y\;{\rm{cm}}} \right)^2}\\
289\;{\rm{c}}{{\rm{m}}^{\rm{2}}} = 49\;{\rm{c}}{{\rm{m}}^{\rm{2}}} + {\left( {y\;{\rm{cm}}} \right)^2} + 14y\;{\rm{c}}{{\rm{m}}^{\rm{2}}} + {\left( {y\;{\rm{cm}}} \right)^2}\\
2{y^2}\;{\rm{c}}{{\rm{m}}^{\rm{2}}} + 14y\;{\rm{c}}{{\rm{m}}^{\rm{2}}} + \left( {49 - 289} \right)\;{\rm{c}}{{\rm{m}}^{\rm{2}}} = 0\\
2{y^2}\;{\rm{c}}{{\rm{m}}^{\rm{2}}} - 14y\;{\rm{c}}{{\rm{m}}^{\rm{2}}} - 240\;{\rm{c}}{{\rm{m}}^{\rm{2}}} = 0
\end{array} $
We will find the roots of the above quadratic equation from the expression given as:
 $ x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $
Here in our equation we have $ \;2 $ for $ a $ , $ - 14 $ for $ b $ and $ {\rm{ - 240}} $ for $ c $ . On substituting these values in this above expression, we get,
 $ \begin{array}{l}
y = \dfrac{{\left( {14} \right) \pm \sqrt {{{\left( {14} \right)}^2} - \left( {4 \times 2 \times - 240} \right)} }}{{2 \times 2}}\\
y = \dfrac{{14 \pm \sqrt {196 + 1920} }}{4}\\
y = \dfrac{{14 \pm 46}}{4}
\end{array} $
Since $ y $ is the side of the triangle and it can not be negative. Therefore, we will consider only positive roots.
  $ \begin{array}{l}
y = \dfrac{{14 + 46}}{4}\\
y = 15
\end{array} $
Hence the value of $ y $ is $ 15\;{\rm{cm}} $ . We will substitute the value of $ y $ in equation (i) to find $ x $ .
 $ \begin{array}{l}
x\;{\rm{cm}} - {\rm{15}}\;{\rm{cm}} = 7\;{\rm{cm}}\\
x = 7\;{\rm{cm}} + {\rm{15}}\;{\rm{cm}}\\
x = 22\;{\rm{cm}}
\end{array} $
 Hence, the other two sides of the triangles are $ {\rm{22}}\;{\rm{cm}} $ and \[{\rm{15}}\;{\rm{cm}}\].

Note: A common mistake that can happen is the misinterpretation of the information given in the question. Since one side is given we need to find the other two sides. We can find the two sides from Pythagora's theorem only since we have two unknowns. Therefore, we will require one more expression to solve the question. This other expression can be written from the data given.