Question

The hypotenuse of a right triangle is \[17{\text{ }}cm\] long. Another side of the triangle is \[7{\text{ }}cm\] longer than the third side. How do you find the unknown side lengths?

Answer 1

Hint: Given, the hypotenuse of a right triangle is \[17{\text{ }}cm\] long and another side of the triangle is \[7{\text{ }}cm\] longer than the third side. So, we will assume the other two sides to be \[x{\text{ }}cm\] and \[\left( {x + 7} \right){\text{ }}cm\]. Then we will apply Pythagoras theorem in the given triangle. We will obtain a quadratic equation in \[x\]. On solving the quadratic equation, we will find the unknown side lengths.

Complete step-by-step answer:
Given, the length of the hypotenuse is \[17{\text{ }}cm\]. Also, given that another side of the triangle is \[7{\text{ }}cm\] longer than the third side. So, we will assume the other two sides to be \[x{\text{ }}cm\] and \[\left( {x + 7} \right){\text{ }}cm\].

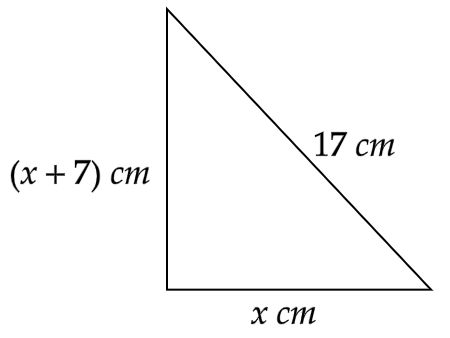
Pythagoras theorem states that the square of the hypotenuse is equal to the sum of the square of the two legs of the right-angle triangle.
Using the Pythagoras theorem, we get
\[ \Rightarrow {\left( {17} \right)^2} = {\left( x \right)^2} + {\left( {x + 7} \right)^2}{\text{ }}\]
On squaring, we get
\[ \Rightarrow 289 = {x^2} + {x^2} + 14x + 49\]
\[ \Rightarrow 289 = 2{x^2} + 14x + 49\]
Subtracting \[49\] from both the sides and on rewriting, we get
\[ \Rightarrow 2{x^2} + 14x = 240\]
\[ \Rightarrow 2{x^2} + 14x - 240 = 0\]
On dividing both the sides by \[2\], we get
\[ \Rightarrow {x^2} + 7x - 120 = 0\]
On splitting the middle term, we get
\[ \Rightarrow {x^2} + 15x - 8x - 120 = 0\]
On taking common, we get
\[ \Rightarrow x\left( {x + 15} \right) - 8\left( {x + 15} \right) = 0\]
\[ \Rightarrow \left( {x - 8} \right)\left( {x + 15} \right) = 0\]
So, we get,
\[ \Rightarrow x = 8\] or \[x = - 15\]
But as we know that length can’t be negative. So, \[x \ne - 15\].
Therefore, we get \[x = 8\] and \[x + 7 = 15\].
Therefore, the lengths of unknown sides are \[8{\text{ }}cm\] and \[{\text{15 }}cm\].

Note: The two perpendicular sides of a right triangle are called the legs. In an isosceles right triangle, the two legs are of equal length. So, the corresponding angles are also congruent. The corresponding angles are \[45\] degrees each. For any right-angle triangle, Pythagoras theorem is the most important formula.