Question

The hydraulic lift is used to lift a car of mass 3000kg. The cross-sectional area of the lift on which the car is supported is \[5\times {{10}^{-2}}m\]. What is the pressure on the smaller piston, if both the pistons are on the same horizontal level?
A. \[6\times {{10}^{5}}Pa\]
B. \[5\times {{10}^{5}}Pa\]
C. \[4\times {{10}^{5}}Pa\]
D. \[3\times {{10}^{5}}Pa\]

Answer 1

Hint: According to Pascal’s Law the pressure exerted at any point in the liquid is transmitted equally throughout the liquid. In accordance with the pascal's law, the pressure at both the pistons of hydraulic lift will be the same. The pressure on the bigger piston can be found with the given information using the formula given below.
Formula used:
\[P=\dfrac{F}{A}\]
\[F=m\times g\]

Complete answer:
According to Pascal’s Law, when the pressure at any point in a confined fluid increases, then there is an equal increase at each and every point in the container confining the liquid. Or in other words, the pressure exerted at any point in the liquid is transmitted equally throughout the liquid.
The hydraulic lift used to lift cars uses Pascal’s Law for this purpose. In these, there is a U-shaped tube with leakproof Pistons at both ends of the tube.

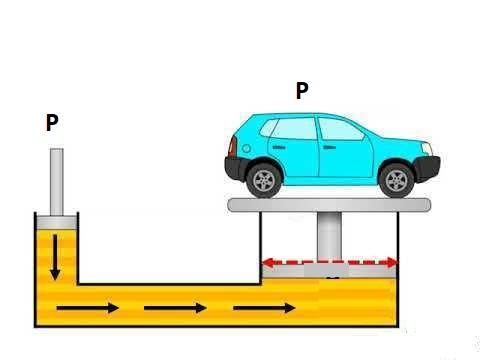
In accordance with the pascal's law, the pressure at both these pistons is the same.
Coming to the question. The weight of the car and the area of the piston supporting it is given.
We know that the pressure is given by
\[P=\dfrac{F}{A}\]
Area A is given, we need to find the force acting on the piston supporting the car. We know that
\[F=m\times g\]
Plugging in known Values
\[\begin{align}
  & F=m\times g \\
 & \Rightarrow F=3000\times 10 \\
 & \Rightarrow F=3\times {{10}^{4}} \\
\end{align}\]
Now,
\[\begin{align}
  & P=\dfrac{F}{A} \\
 & \Rightarrow P=\dfrac{3\times {{10}^{4}}}{5\times {{10}^{-2}}} \\
 & \Rightarrow P=6\times {{10}^{5}}Pa \\
\end{align}\]
The pressure on the bigger piston is \[6\times {{10}^{5}}Pa\]and according to Pascal's Law, the same pressure would be on the smaller piston.
 Therefore, the pressure on the smaller piston is \[6\times {{10}^{5}}Pa\]

So, the correct answer is “Option A”.

Note:
Pascal’s Law was named after the guy who proposed it, Blaise Pascal. He was a French Physicist and Mathematician. He got the basics of his law when he observed that the water in a container stays at the same horizontal level and thus must have the same amount of pressure acting on it. He further researched his observation to give us Pascal's Law. This law has many real-world utilities like hydraulic lifts, jacks and breaks etc.