Question

The half-life of a radioactive element X is equal to the average life of other element Y. Initially, the number of atoms in both of them is the same. Then,
A. Initially the rate of disintegration of X and Y would be the same.
B. X and Y disintegrate with the same rate, always
C. Initially the rate of disintegration of Y would be greater than that of X.
D. Initially the rate of disintegration of X would be greater than that of Y.

Answer 1

Hint: In the above question, it is given that the half-life of radioactive element X equals the average life of radioactive element Y. Therefore, equating the formulae of half-life of X and average life of Y would give us an inequality which answers the above question.

Complete answer:
As we know that it’s a property of a radioactive element to decay into a smaller nuclei because of its unstable nuclei and to gain stability.Now half-life of a substance is that time in which exactly half of number of nuclei of radioactive elements from sample decays into smaller nuclei (nuclei of another element). It is represented by \[{t_{\dfrac{1}{2}}}\](mean ‘t’ subscript \[\dfrac{1}{2}\]).
Also, if \[{N_0}\]is the total no of atoms at t=0 (initially)
Then after half life time, no. of atoms = \[\dfrac{{{N_0}}}{2}\]

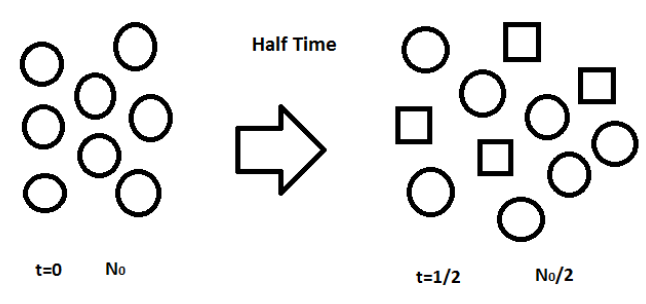
Circle represents the nuclei of X element. Rectangles represent the nuclei of any other element in which radioactive element decay.
Mathematically, Half-life time is given by \[{t_{\dfrac{1}{2}}} = \dfrac{{0.693}}{{\mathbf{\lambda }}}\]
Whereas, Mean life of a substance is the average time in which exactly all the nuclei of radioactive element from a sample decays completely into its smaller nuclei. It is represented by τ (tau).
Also, if \[{N_0}\]is the total no of atoms at t=0 (initially)
Then after mean life, no. of atoms = 0
\[\tau = \dfrac{1}{{\mathbf{\lambda }}}\] [Refers to the derivation of mean life time].
So, for element ‘X’, half life time is given by\[{\left( {{t_{\dfrac{1}{2}}}} \right)_X} = \dfrac{{0.693}}{{{{\mathbf{\lambda }}_X}}}\].
Where \[{{\mathbf{\lambda }}_X}\]= decay constant of element X.
And for element Y, average time is given by \[{{\mathbf{\tau }}_Y} = \dfrac{1}{{{{\mathbf{\lambda }}_Y}}}\]
Where \[{{\mathbf{\lambda }}_Y}\]=decay constant of element.

Now, given in the question, the half-life of a radioactive element X is equal to the average life of other element Y.
\[
{\left( {{t_{\dfrac{1}{2}}}} \right)_X} = {{\mathbf{\tau }}_Y} \\
\Rightarrow \dfrac{{0.693}}{{{{\mathbf{\lambda }}_X}}} = \dfrac{1}{{{{\mathbf{\lambda }}_Y}}} \\
\Rightarrow {{\mathbf{\lambda }}_y} = \dfrac{{{{\mathbf{\lambda }}_X}}}{{0.693}} \\
\Rightarrow {{\mathbf{\lambda }}_Y} = {{\mathbf{\lambda }}_X} \times 1.44 \\
\therefore {{\mathbf{\lambda }}_Y} > {{\mathbf{\lambda }}_X}
 \]
So the decay constant of element Y is greater than the element X, thus, element Y would disintegrate faster and quickly as compared to X.

Hence, option C is correct.

Note:Don’t get confused with the number of atoms. Since the average life and half life time of a radioactive element depends upon the decay constant of an element and not on the numbers of atoms. The disintegration constants for elements ‘X’ and ‘Y’ have different values and should not be confused to be the same.