Question

The given point $P$ is a point which moves in the \[x-y\] plane such that the point $P$ is nearer to the centre of a square than any of the sides. The four vertices of the square are $\left( \pm a,\pm a \right)$. The region in which $P$ will move is bounded by parts of parabolas of which one has the equation
a.${{y}^{2}}={{a}^{2}}+2ax$
b.${{x}^{2}}={{a}^{2}}+2ay$
c.${{y}^{2}}+2ax={{a}^{2}}$
d.None of these

Answer 1

Hint: To solve this question, drawing a figure with all details is necessary. The distances can be found out using the distance formula as well as by subtracting or adding the coordinates.

Complete step-by-step answer:
The vertices of the square are given in the question as $\left( \pm a,\pm a \right)$. Let point $P$ have coordinates as $\left( x,~y \right)$.
A plot is made with the square and the point P in the \[x-y\] plane, taken in the first quadrant.

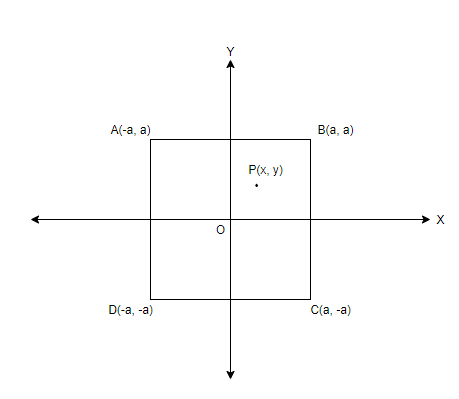
Next step is to mark the distance $a$ of the square in the plot. Then mark the distances $x$ and $y$ corresponding to the coordinates of point $P$. Consider points \[E\] and \[F\] to sides of the square \[BC\] and $AB$ respectively, as shown below,

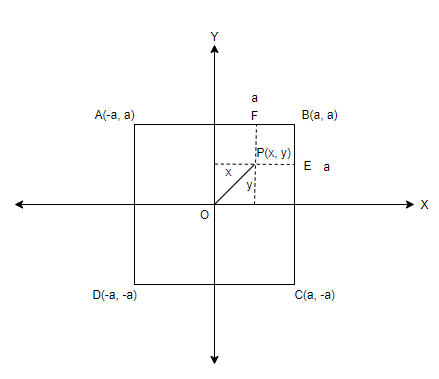
The distance of the point $P$ having coordinates $\left( x,~y \right)$ to the centre \[O\], i.e. the origin can be written using the distance formula as,
$OP=\sqrt{{{x}^{2}}+{{y}^{2}}}$
The distance from point $P$ to the sides \[BC\] and $AB$ is given by $PE$ and \[PF\] respectively. The distances can be obtained by subtracting the coordinates that are given in terms of $x,~y$ and $a$ by referring to the plot. The distances are,
$PE=x$ coordinate of $E-x$ coordinate of $P=\left| \left( a-x \right) \right|$
$PF=y$ coordinate of $F-y$ coordinate of $P=\left| \left( a-y \right) \right|$
It is said in the question that the point $P$ is nearer to the centre than to the sides.
Therefore, we have the relation as,
$PE>OP~\And ~PF>OP$
So, we can formulate two equations by substituting the distances as,
$\left| \left( a-x \right) \right|>\sqrt{{{x}^{2}}+{{y}^{2}}}\ldots \ldots \ldots ~~\left( i \right)$
$\left| \left( a-y \right) \right|>\sqrt{{{x}^{2}}+{{y}^{2}}}\ldots \ldots \ldots ~~\left( ii \right)$
Now, we have to consider the distances to the other two sides also, so consider another set of points $G$ and \[H\], as shown below,

The distance from point $P$ to the sides $AD$ and \[DC\] is given by $PG$ and \[PH\] respectively. The distances can be obtained by subtracting the coordinates that are given in terms of $x,~y$ and $a$ by referring to the plot. The distances are,
$PG=x$ coordinate of $G-x$ coordinate of $P=\left| \left( -a-x \right) \right|=\left| \left( a+x \right) \right|$
$PH=y$ coordinate of $H-y$ coordinate of $P=\left| \left( -a-y \right) \right|=\left| \left( a+y \right) \right|$
As per the condition in the question that the point $P$ is nearer to the centre than to the sides, we have the relation as,
$PG>OP~\And ~PH>OP$
So, we can formulate two equations by substituting the distances as,
$\left| \left( a+x \right) \right|>\sqrt{{{x}^{2}}+{{y}^{2}}}\ldots \ldots \ldots ~~\left( iii \right)$
$\left| \left( a+y \right) \right|>\sqrt{{{x}^{2}}+{{y}^{2}}}\ldots \ldots \ldots ~~\left( iv \right)$
We have four equations $\left( i \right),~\left( ii \right),~\left( iii \right)$ and $\left( iv \right)$. The region in which $P$ will be bounded by parts of parabola can be found by simplifying the four equations.
Squaring and equating both sides of the equations $\left( i \right),~\left( ii \right),~\left( iii \right)$ and $\left( iv \right)$,
$\left( i \right)~\ldots \ldots \ldots ~~{{\left| \left( a-x \right) \right|}^{2}}={{\sqrt{{{x}^{2}}+{{y}^{2}}}}^{2}}$
${{a}^{2}}+{{x}^{2}}-2ax={{x}^{2}}+{{y}^{2}}$
${{y}^{2}}={{a}^{2}}-2ax\ldots \ldots \ldots ~~\left( v \right)$

$\left( ii \right)\ldots \ldots \ldots ~~{{\left| \left( a-y \right) \right|}^{2}}={{\sqrt{{{x}^{2}}+{{y}^{2}}}}^{2}}$
${{a}^{2}}+{{y}^{2}}-2ay={{x}^{2}}+{{y}^{2}}$
${{x}^{2}}={{a}^{2}}-2ay\ldots \ldots \ldots ~~\left( vi \right)$
$\left( iii \right)\ldots \ldots \ldots ~~{{\left| \left( a+x \right) \right|}^{2}}={{\sqrt{{{x}^{2}}+{{y}^{2}}}}^{2}}$
${{a}^{2}}+{{x}^{2}}+2ax={{x}^{2}}+{{y}^{2}}$
${{y}^{2}}={{a}^{2}}+2ax\ldots \ldots \ldots ~~\left( vii \right)$
$\left( iv \right)\ldots \ldots \ldots ~~{{\left| \left( a+y \right) \right|}^{2}}={{\sqrt{{{x}^{2}}+{{y}^{2}}}}^{2}}$
${{a}^{2}}+{{y}^{2}}+2ay={{x}^{2}}+{{y}^{2}}$
${{x}^{2}}={{a}^{2}}+2ay\ldots \ldots \ldots ~~\left( viii \right)$
Therefore, the equations $\left( v \right),~\left( vi \right),~\left( vii \right)$ and $\left( viii \right)$ represent the equations of the parts of parabolas that the point $P$ is bounded by. They are,
${{y}^{2}}={{a}^{2}}-2ax$
${{x}^{2}}={{a}^{2}}-2ay$
${{y}^{2}}={{a}^{2}}+2ax$
${{x}^{2}}={{a}^{2}}+2ay$
Therefore, by looking at the options, we get options a,b and c as the correct answers.
Option a, b and c
Note: In the question, the point $P$ lies in the \[x-y\] plane, so the point can be considered in any quadrant in the plot. The coordinates and hence the distances would change accordingly for the sides of the square considered. Ultimately, the final answer would be the same.