Question

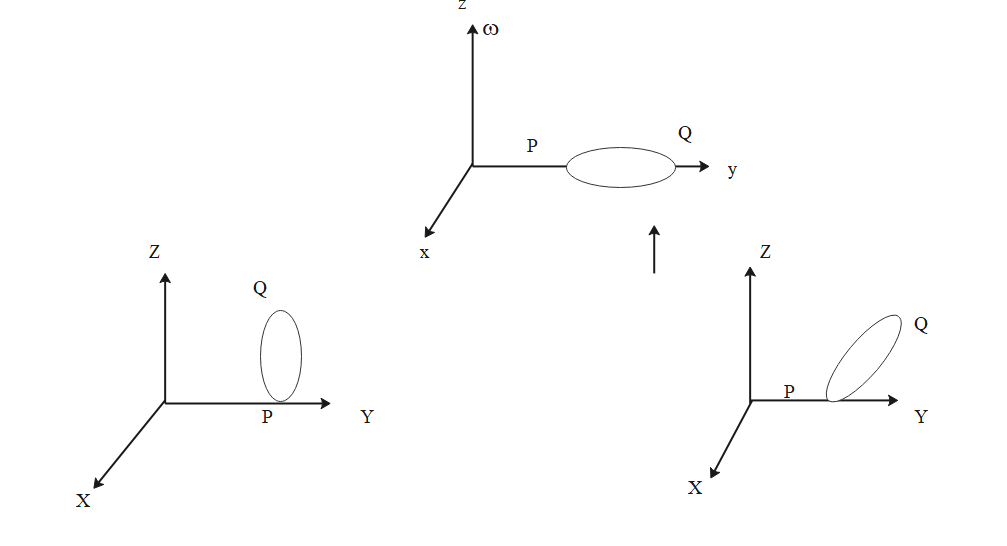
The general motion of a rigid body can be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous axis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless stick, as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed $\omega $, the motion at any instant can be taken as a combination of (i) a rotation of the centre of mass of the disc about the z-axis, and (ii) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points p and q). Both these motions have the same angular speed $\omega $ in this case.

Now consider two similar systems as shown in the figure: case (a) the disc with its face vertical and parallel to the x-z plane; case (b) the disc with its face making an angle of 45 degree with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point p, and the systems are rotated with constant angular speed $\omega $ about the z-axis.
Which of the following is true about the instantaneous axis passing through the centre of mass?
A) it is vertical for both the cases
B) it is vertical for case a; and is 45 degree to the x-z plane and lies in the plane of the disc for case (b).
C)it is horizontal in case (a); and is at 45 degree to the x-z plane and is normal to the plane of the disc for case (b).
D)it is vertical for case (a); and is at 45 degree to the x-z plane and is normal to the plane of the disc for case (b).

Answer 1

Hint: Assume the position vectors and velocity vectors of the centre of the disc and any other point a on the disc. Find the relation between the position vectors of two points and the velocity vectors. Then, consider the motion about the instantaneous axis and verify the options.

Complete answer:
Let c be the centre of the disc with position vector ${{\vec{r}}_{c}}$ and velocity vector ${{\vec{v}}_{c}}$. Let a be a general point on the disc having position vector ${{\vec{r}}_{a}}$. Let $\vec{\omega }$be the angular velocity of the system as given in the problem and $\vec{\omega }'$ be the angular velocity about the instantaneous axis. The velocity of point c and point a are given by ${{\vec{v}}_{a}}=\vec{\omega }\times {{\vec{r}}_{a}}$ hand ${{\vec{v}}_{c}}=\vec{\omega }'\times {{r}_{c}}$. Also, considering the motion about the instantaneous axis,
${{\vec{v}}_{a}}={{\vec{v}}_{c}}+\vec{\omega }'\times ({{\vec{r}}_{a}}-{{\vec{r}}_{c}})$
Substitute ${{\vec{v}}_{a}}$value in the above equation, we get
$(\vec{\omega }'-\vec{\omega })\times ({{r}_{a}}-{{r}_{c}})=0$
Now, as the radius vector is any general vector on the disc, the above equation is satisfied only when $\vec{\omega }'=\vec{\omega }$. This argument will be true for both cases. Therefore, the instantaneous axis for both the cases are parallel to the z axis and angular speed about these aces are equal.

Correct option is option a.

Additional information:
Rigid body is an idealization of a solid body where the deformations occurring on the body are neglected. In other words, the distance between any 2 given points of rigid body remains constant regardless of the external force acting upon it. The concept of rigid body and rigid body dynamics was developed to solve a range of problems that could not be explained with classical physics. Best examples to demonstrate this is the motion of rotation of the fan, a potter’s wheel, etc. Which we cannot explain by assuming mass. In real life in the case of a body such as wheels and steel rods, bending is negligible, so we treat those bodies as a rigid body.

Note:
A system which can have translational and rotational motion, when rotated with an angular speed, the motion at any instant can be taken as a combination of rotation of the centre of mass of the disc about any axis, rotation of the disc through an instantaneous vertical axis passing through centre of mass.