-
Courses-
Crash Courses 2021
-
Olympiads/NTSE/Others
-
Micro Courses
-
Vedantu Super Kids NEW
-
Reading & Spoken English -
FREEMaster Classes
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
Questions & Answers
Question
Answers
Related Questions
The function $f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$
A. is a constant function
B. has a domain$\left( 0,1 \right)\bigcup \left( e,\infty \right)$
C. is such that $\underset{x\to 1}{\mathop{\lim }}\,f\left( x \right)$
D. is aperiodic
Answer
![Verified]()
Verified
Verified
Hint: First try to simplify the given function $f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$.Then proceeds to the options provided to verify one by one. Here, aperiodic means irregularity.
Complete step-by-step answer:
Here, we have a function given as$f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}\ldots \ldots (1)$.
We need to find correct answer/answers by observing all the options given.
Now, Option A. is given as ${{x}^{\dfrac{1}{\ln x}}}$is a constant function.
We can verify this option by just simplifying the function $f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$given in the problem.
We have $f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$
Taking log to both sides, we get
\[{{\log }_{e}}\left( f\left( x \right) \right)={{\log }_{e}}{{\left( x \right)}^{\dfrac{1}{\ln x}}}\ldots \ldots (2)\]
We know property of log as
$\log {{m}^{n}}=n\log m$
So, we can write equation (2) as
\[{{\log }_{e}}\left( f\left( x \right) \right)=\dfrac{1}{\ln x}{{\log }_{e}}\left( x \right)\]
Here ${{\log }_{e}}x$ has base ‘e’ and we know that $\ln x={{\log }_{e}}x$(same value with different representations).
${{\log }_{e}}\left( f\left( x \right) \right)=1$
Now, we know that if
${{\log }_{a}}N=x$, then
\[N={{a}^{x}}\]
Hence,${{\log }_{e}}\left( f\left( x \right) \right)=1$, can be written as
$\begin{align}
& f\left( x \right)=e'=e \\
& f\left( x \right)=e \\
\end{align}$
Hence, given function f(x) is ‘e’ i.e. Constant function.
So, Option A is correct.
Now, Coming to option B. i.e. f(x) has a domain$\left( 0,1 \right)\bigcup \left( e,\infty \right)$.
To verify option ‘B’, we need to calculate the domain of$f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$.
The given function is in volument of ‘$\ln x$’. So, we cannot put negative values to a given function f(x) because the domain of $\ln x$ is ${{R}^{+}}$or$\left( 0,\infty \right)$.
We know the value of ln1 is 0. So, $\dfrac{1}{\ln x}$cannot take x=1 as well because $\dfrac{1}{0}$is not defined.
Hence, domain of ${{\left( x \right)}^{\dfrac{1}{\ln x}}}$ is$\left( 0,1 \right)\bigcup \left( e,\infty \right)$.
So, option B. is not the correct answer.
Now, to verify option ‘C’ i.e. function $f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$ is such that $\underset{x\to 1}{\mathop{\lim }}\,f\left( x \right)$ exist,
We need to calculate LHL and RHL for x=1 i.e. $x\to {{1}^{-}}$and$x\to {{1}^{+}}$.
Now, we have already calculated that $f\left( x \right)=e$ for the domain$\left( 0,1 \right)\bigcup \left( e,\infty \right)$.
So, $\ln x$ LHL ($x\to {{1}^{-}}$) and RHL ($x\to {{1}^{+}}$).
We have constant function ‘e’. So the limit at $x\to 1$will exist.
So, option C. is the correct answer.
As ${{\left( x \right)}^{\dfrac{1}{\ln x}}}$ is simplified to ‘e’.
Hence graph of given function i.e.
$f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$Is given as
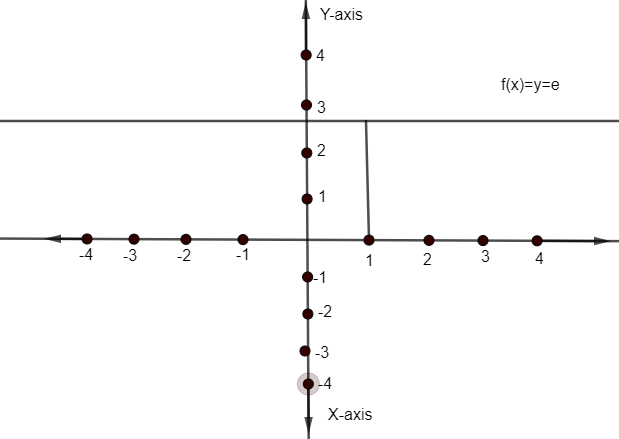
Hence, a given function is aperiodic as well where aperiodic means irregularity or not periodic function.
Hence option D. is also correct.
Note: One can go wrong if he/she will not simplify the given relation. As one can think that a given function is written in terms of ‘x’ so how it could be a constant function. So, be careful with these kinds of problems.
One can go wrong with the domain of${{\left( x \right)}^{\dfrac{1}{\ln x}}}$. As domain of ${{x}^{a}}$is ‘R’ i.e. All real numbers. So, one can get confused with it. So, checking domain for $\dfrac{1}{\ln x}$is the key point for calculation of domain of$f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$.
Complete step-by-step answer:
Here, we have a function given as$f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}\ldots \ldots (1)$.
We need to find correct answer/answers by observing all the options given.
Now, Option A. is given as ${{x}^{\dfrac{1}{\ln x}}}$is a constant function.
We can verify this option by just simplifying the function $f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$given in the problem.
We have $f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$
Taking log to both sides, we get
\[{{\log }_{e}}\left( f\left( x \right) \right)={{\log }_{e}}{{\left( x \right)}^{\dfrac{1}{\ln x}}}\ldots \ldots (2)\]
We know property of log as
$\log {{m}^{n}}=n\log m$
So, we can write equation (2) as
\[{{\log }_{e}}\left( f\left( x \right) \right)=\dfrac{1}{\ln x}{{\log }_{e}}\left( x \right)\]
Here ${{\log }_{e}}x$ has base ‘e’ and we know that $\ln x={{\log }_{e}}x$(same value with different representations).
${{\log }_{e}}\left( f\left( x \right) \right)=1$
Now, we know that if
${{\log }_{a}}N=x$, then
\[N={{a}^{x}}\]
Hence,${{\log }_{e}}\left( f\left( x \right) \right)=1$, can be written as
$\begin{align}
& f\left( x \right)=e'=e \\
& f\left( x \right)=e \\
\end{align}$
Hence, given function f(x) is ‘e’ i.e. Constant function.
So, Option A is correct.
Now, Coming to option B. i.e. f(x) has a domain$\left( 0,1 \right)\bigcup \left( e,\infty \right)$.
To verify option ‘B’, we need to calculate the domain of$f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$.
The given function is in volument of ‘$\ln x$’. So, we cannot put negative values to a given function f(x) because the domain of $\ln x$ is ${{R}^{+}}$or$\left( 0,\infty \right)$.
We know the value of ln1 is 0. So, $\dfrac{1}{\ln x}$cannot take x=1 as well because $\dfrac{1}{0}$is not defined.
Hence, domain of ${{\left( x \right)}^{\dfrac{1}{\ln x}}}$ is$\left( 0,1 \right)\bigcup \left( e,\infty \right)$.
So, option B. is not the correct answer.
Now, to verify option ‘C’ i.e. function $f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$ is such that $\underset{x\to 1}{\mathop{\lim }}\,f\left( x \right)$ exist,
We need to calculate LHL and RHL for x=1 i.e. $x\to {{1}^{-}}$and$x\to {{1}^{+}}$.
Now, we have already calculated that $f\left( x \right)=e$ for the domain$\left( 0,1 \right)\bigcup \left( e,\infty \right)$.
So, $\ln x$ LHL ($x\to {{1}^{-}}$) and RHL ($x\to {{1}^{+}}$).
We have constant function ‘e’. So the limit at $x\to 1$will exist.
So, option C. is the correct answer.
As ${{\left( x \right)}^{\dfrac{1}{\ln x}}}$ is simplified to ‘e’.
Hence graph of given function i.e.
$f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$Is given as
Hence, a given function is aperiodic as well where aperiodic means irregularity or not periodic function.
Hence option D. is also correct.
Note: One can go wrong if he/she will not simplify the given relation. As one can think that a given function is written in terms of ‘x’ so how it could be a constant function. So, be careful with these kinds of problems.
One can go wrong with the domain of${{\left( x \right)}^{\dfrac{1}{\ln x}}}$. As domain of ${{x}^{a}}$is ‘R’ i.e. All real numbers. So, one can get confused with it. So, checking domain for $\dfrac{1}{\ln x}$is the key point for calculation of domain of$f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$.
×
Sorry!, This page is not available for now to bookmark.
Like this
Liked
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
