Question

The function $f\left( x \right) = {x^3} - 3{x^2} - 24x + 5$ is an increasing function in the interval given below.
A) $\left( { - \infty , - 2} \right) \cup \left( {4,\infty } \right)$
B) $\left( { - 2,\infty } \right)$
C) $\left( { - 2,4} \right)$
D) $\left( { - \infty ,4} \right)$

Answer 1

Hint: The given problem revolves around the nature of the curve, its slope and concavity. The increasing and decreasing nature of the curve is judged by its first derivative as it gives an idea about the slope of the curve. If the first derivative of a function is positive in a certain interval, then the function is increasing in that interval. If the derivative of the function is negative, then the function is decreasing in that interval.

Complete step-by-step solution:
Consider, $f\left( x \right) = {x^3} - 3{x^2} - 24x + 5$.
So, to find the increasing or decreasing nature of a curve, we have to find the variation of slope of the curve. To find critical points, we need to find the first order derivative of f(x).
$f\left( x \right) = {x^3} - 3{x^2} - 24x + 5$
Using the power rule of differentiation as $\dfrac{{d\left( {{x^n}} \right)}}{{dx}} = n{x^{n - 1}}$, we get,
\[ \Rightarrow f'\left( x \right) = 3{x^2} - 3\left( {2x} \right) - 24\]
\[ \Rightarrow f'\left( x \right) = 3{x^2} - 6x - 24\]
Now equate the derivative function equal to zero to find critical points of a function where the function actually changes its nature from increasing to decreasing or vice versa.
\[ \Rightarrow f'\left( x \right) = 3{x^2} - 6x - 24 = 0\]
Dividing both sides of equation by here, we get,
\[ \Rightarrow {x^2} - 2x - 8 = 0\]
Factorise, by splitting of middle term
\[ \Rightarrow {x^2} - 4x + 2x - 8 = 0\]
Taking common terms outside the bracket, we get,
\[ \Rightarrow x\left( {x - 4} \right) + 2\left( {x - 4} \right) = 0\]
\[ \Rightarrow \left( {x + 2} \right)\left( {x - 4} \right) = 0\]
Either \[\left( {x + 2} \right) = 0\] or \[\left( {x - 4} \right) = 0\].
So Either \[x = - 2\] or \[x = 4\].
So, critical points are $x = - 2,4$.
These two values of x divide R (Real number set) into three disjoint intervals, namely $\left( { - \infty , - 2} \right)$,$( - 2,4)$ and $(4,\infty )$.

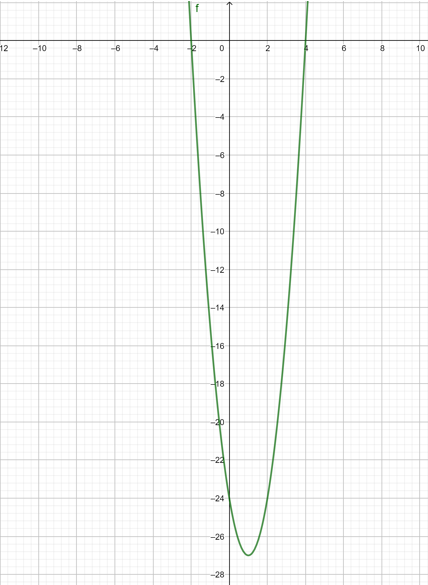
Now we observe the sign of the first derivative $f'(x)$ in these intervals.
Now, $x \in \left( { - \infty , - 2} \right)$ or \[x \in \left( { - 2,3} \right)\] or \[x \in \left( {3,\infty } \right)\]
For $x \in \left( { - \infty , - 2} \right)$, we have, $f'(x) > 0$. Thus the given function f(x) is increasing in this interval.
For \[x \in ( - 2,4)\], we have, $f'(x) < 0$. Thus the given function f(x) is decreasing in this interval.
For \[x \in (4,\infty )\], we have, $f'(x) > 0$. Thus the given function f(x) is increasing in this interval.
So, the function $f\left( x \right) = {x^3} - 3{x^2} - 24x + 5$ is increasing for $\left( { - \infty , - 2} \right) \cup \left( {4,\infty } \right)$.

Note: The first derivative test comes into use to find the increasing and decreasing nature of a function. The intervals where the derivative of function is positive indicates that the value of function is increasing with the value of variable. Similarly, the intervals where the derivative of function is negative, the function decreases with the increasing value of variable.