
The freezing point of a solution containing 0.3 grams of acetic acid in 30 gms of benzene is lowered by 0.45 K. Calculate the Van’t Hoff factor. (at. wt. of $\text{C}$ = 12, $\text{O}$ = 16, $\text{H}$ = 1, ${{\text{K}}_{\text{f}}}$ for benzene = $5.12\text{ K kg mol}{{\text{e}}^{-1}}$ )
Answer
573.9k+ views
Hint: Van’t Hoff factor is the measure of particles present after dissociation divided by the number of particles present initially. It is represented by ‘i’ and has the formula $\dfrac{\text{particles after dissociation/association}}{\text{particles before dissociation/association}}$ . If van’t Hoff factor is greater than 1, then dissociation occurs. If its value is less than 1, then association occurs and if van’t Hoff factor is equal to 1, then neither dissociation nor association occurs.
Complete answer:
Step (1)- Write the formula: Considering as an ideal solution, the depression in freezing point depends on the solute concentration that is e expressed as $\vartriangle {{\text{T}}_{\text{f}}}={{\text{K}}_{\text{f}}}\times \text{m}\times \text{i}$; where
- $\vartriangle {{\text{T}}_{\text{f}}}$ is the freezing-point depression expressed as${{\text{T}}_{\text{f}}}$ (pure solvent) − ${{\text{T}}_{\text{f}}}$(solution).
- ${{\text{K}}_{\text{f}}}$ is the cryoscopic constant which only depends on the properties of the solvent.
- $\text{m}$ is the molality which is represented as moles solute per kilogram of solvent or $\dfrac{\text{moles of solute}}{\text{mass of solvent in kg}}$.
- $\text{i}$ is van't Hoff factor.
Step (2)- Find molality by finding the moles of acetic acid; moles are defined as the weight of substance per molar mass of it. Its formula is$\text{moles=}\dfrac{\text{mass of substance}}{\text{molar mass}}$. Molar mass of acetic acid $\left( \text{C}{{\text{H}}_{3}}\text{COOH} \right)$:
- Atomic mass of $\text{C}$ is 12 grams.
- Atomic mass of $\text{H}$ is 1 gram.
- Atomic mass of $\text{O}$ is 16 grams.
Molar Mass is $\left[ \left( 12\times 2 \right)+\left( 1\times 4 \right)+\left( 16\times 2 \right) \right]$ or 60 grams.
Step (3)- Write the values given in the question; mass of acetic acid is given as 0.3 grams and mass of benzene (solvent) = 30g, $\vartriangle {{\text{T}}_{\text{f}}}=0.45\text{K}$ and ${{\text{K}}_{\text{f}}}$ for benzene = $5.12\text{ K kg mol}{{\text{e}}^{-1}}$.
Step (4)- The molality becomes $\dfrac{0.3\times \text{1000}}{60\times 30}$. The term is divided by 1000 because we have to find per ‘kg’ of solvent. The value of molality is 0.167 m.
Step (5)- Put the value of m in the formula $\vartriangle {{\text{T}}_{\text{f}}}={{\text{K}}_{\text{f}}}\times \text{m}\times \text{i}$; so, $0.45=5.12\times 0.167\times \text{i}$, van’t Hoff factor is 0.527.
The correct answer is van’t Hoff factor is 0.527.
Note: The value of Van’t Hoff factor obtained is nearing the actual experimental value of i for acetic acid. Van’t Hoff factor is nearly 0.5. [acetic acid has the tendency to dimerize (two molecules combine), so the number of particles after association is 1 and before association is 2. The van’t Hoff factor will be $\dfrac{1}{2}=0.5$]. So, the correct answer can be interpreted easily just by knowing that acetic acid will dimerize. The dimerization of acetic acid looks like
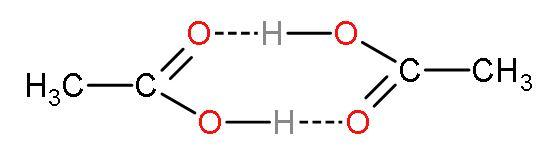
Complete answer:
Step (1)- Write the formula: Considering as an ideal solution, the depression in freezing point depends on the solute concentration that is e expressed as $\vartriangle {{\text{T}}_{\text{f}}}={{\text{K}}_{\text{f}}}\times \text{m}\times \text{i}$; where
- $\vartriangle {{\text{T}}_{\text{f}}}$ is the freezing-point depression expressed as${{\text{T}}_{\text{f}}}$ (pure solvent) − ${{\text{T}}_{\text{f}}}$(solution).
- ${{\text{K}}_{\text{f}}}$ is the cryoscopic constant which only depends on the properties of the solvent.
- $\text{m}$ is the molality which is represented as moles solute per kilogram of solvent or $\dfrac{\text{moles of solute}}{\text{mass of solvent in kg}}$.
- $\text{i}$ is van't Hoff factor.
Step (2)- Find molality by finding the moles of acetic acid; moles are defined as the weight of substance per molar mass of it. Its formula is$\text{moles=}\dfrac{\text{mass of substance}}{\text{molar mass}}$. Molar mass of acetic acid $\left( \text{C}{{\text{H}}_{3}}\text{COOH} \right)$:
- Atomic mass of $\text{C}$ is 12 grams.
- Atomic mass of $\text{H}$ is 1 gram.
- Atomic mass of $\text{O}$ is 16 grams.
Molar Mass is $\left[ \left( 12\times 2 \right)+\left( 1\times 4 \right)+\left( 16\times 2 \right) \right]$ or 60 grams.
Step (3)- Write the values given in the question; mass of acetic acid is given as 0.3 grams and mass of benzene (solvent) = 30g, $\vartriangle {{\text{T}}_{\text{f}}}=0.45\text{K}$ and ${{\text{K}}_{\text{f}}}$ for benzene = $5.12\text{ K kg mol}{{\text{e}}^{-1}}$.
Step (4)- The molality becomes $\dfrac{0.3\times \text{1000}}{60\times 30}$. The term is divided by 1000 because we have to find per ‘kg’ of solvent. The value of molality is 0.167 m.
Step (5)- Put the value of m in the formula $\vartriangle {{\text{T}}_{\text{f}}}={{\text{K}}_{\text{f}}}\times \text{m}\times \text{i}$; so, $0.45=5.12\times 0.167\times \text{i}$, van’t Hoff factor is 0.527.
The correct answer is van’t Hoff factor is 0.527.
Note: The value of Van’t Hoff factor obtained is nearing the actual experimental value of i for acetic acid. Van’t Hoff factor is nearly 0.5. [acetic acid has the tendency to dimerize (two molecules combine), so the number of particles after association is 1 and before association is 2. The van’t Hoff factor will be $\dfrac{1}{2}=0.5$]. So, the correct answer can be interpreted easily just by knowing that acetic acid will dimerize. The dimerization of acetic acid looks like

Recently Updated Pages
Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE




