Question

The equivalent inductance of two inductors is 2.4H when connected in parallel 10H when connected in series. The difference between two inductances is (Neglecting mutual inductance):
A. 2H
B. 3H
C. 4H
D. 5H

Answer 1

Hint: Inductance coil is an electrical element of a circuit which stores the electrical energy in the form of magnetic field. Like resistance and capacitor, inductance is also a passive element because it delivers the energy but not on a continuous basis. Inductors are attached in the circuit in series and parallel to each other.

Formula used: In series: $L_{total} = L_1+L_2+L_3+ . . .$

In parallel:$\dfrac1{L_{total}} = \dfrac1L_1 +\dfrac1L_2+\dfrac1L_3+ . . .$

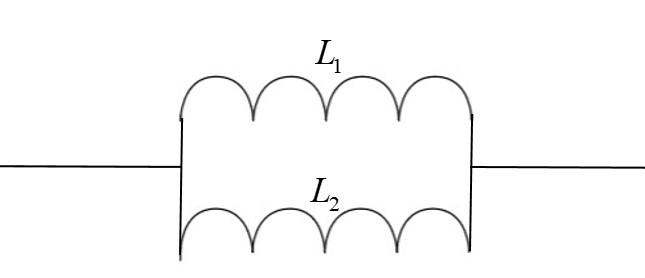
Complete step by step answer:
Let the inductance of the first inductor be $L_1$ and that of second is $L_2$. Here we should keep in mind that we are asked to find the value of difference in inductances, hence proceeding in that way. As we know if the inductors are connected in series, the net inductance of the combination is $L_{total} = L_1+L_2$
Hence,$L_1+L_2 = 10$ …….①
And in parallel, $\dfrac1L_1 +\dfrac1L_2 = \dfrac{1}{2.4}$
Or $\dfrac{L_1+L_2}{L_1\times L_2} = \dfrac1{2.4}$
Or $L_1L_2 = 2.4\times 10 = 24$ [ from ①]
Now, from ①, we have
$(L_1+L_2)^2=100$
Or $L_1^2 + L_2^2 +2L_1L_2 =100$
Or $L_1^2+L_2^2 - 2L_1L_2 + 4L_1L_2 = 100$
Or $(L_1 - L_2)^2 + 4L_1L_2 = 100$
Now, as $L_1L_2 =24$
Hence, $(L_1 - L_2)^2 = 100 - 4\times 24 = 100 - 96 = 4H$
Thus, $L_1 - L_2 = \sqrt 4 = 2H$
Hence we can see that the difference between the two inductor values is 2H.

So, the correct answer is “Option A”.

Note: In the question, we are directed to neglect the mutual inductance but practically, we have the mutual inductances between the coils especially if the distances between the inductors is less. Hence if not given to neglect, we have to consider the mutual inductance too. One must be aware that inductors and resistors are similar in the fact that in series, both resistors and inductors are added algebraically to get net value to resistance or inductance and for parallel combination, the reciprocal sum will give the reciprocal of total resistance and inductance of the system.