Question

The equation of image of the line $\dfrac{x-1}{9}=\dfrac{y-2}{-1}=\dfrac{z+3}{-3}$ in the plane $3x-3y+10z=26$ is:
A. $\dfrac{x-4}{9}=\dfrac{y+1}{-1}=\dfrac{z-7}{3}$
B. $\dfrac{x-4}{9}=\dfrac{y+1}{-1}=\dfrac{z-7}{-3}$
C. $\dfrac{x+4}{9}=\dfrac{y+1}{-1}=\dfrac{z-7}{-3}$
D. $\dfrac{x-4}{9}=\dfrac{y-1}{-1}=\dfrac{z-7}{-3}$

Answer 1

Hint: So, here in the above question we can get an idea about how the image of line i.e. $\dfrac{x-1}{9}=\dfrac{y-2}{-1}=\dfrac{z+3}{-3}$ in the plane $3x-3y+10z=26$ first upon we have to find the intersection point and then let $\lambda $ as the constant with this we will get the values of x, y, z then we will put this in the plane equation and then we will whether it is satisfying or not then we will find the values of a, b, c this will lead us to the final answer this a very detailed method I’ll give you the short method in Note as well.

Complete step-by-step solution:
So, let consider one plane and line is passing through it and we want to find the image of that line so how we find that image lets see. Now, the line is passing through at the plane point above the line is P (1, 2, -3).

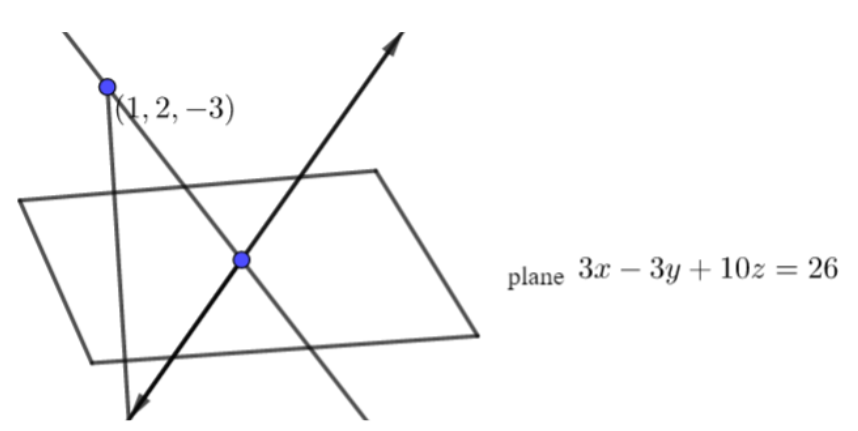
So, first we find the intersection point,
Let’s take $\dfrac{z+3}{-3}=\lambda $
$\begin{align}
  &\Rightarrow x=9\lambda +1 \\
 &\Rightarrow y=-\lambda +2 \\
 &\Rightarrow z=-3\lambda -3 \\
\end{align}$
So, we get the general point at P(1, 2, -3) and if this all equations of x. y, z are satisfied on that point then we get an intersection point.
Substituting in \[3x-3y+10z-26=0\] then we will get,
$\begin{align}
&\Rightarrow 3\left( 9\lambda +1 \right)-3\left( -\lambda +2 \right)+10\left( -3\lambda -3 \right)-26=0 \\
&\Rightarrow 27\lambda +3+3\lambda -6-30\lambda -30-26=0 \\
&\Rightarrow 59\ne 0 \\
\end{align}$
it means the line is not passing through that point and this case will be parallel to the plane.

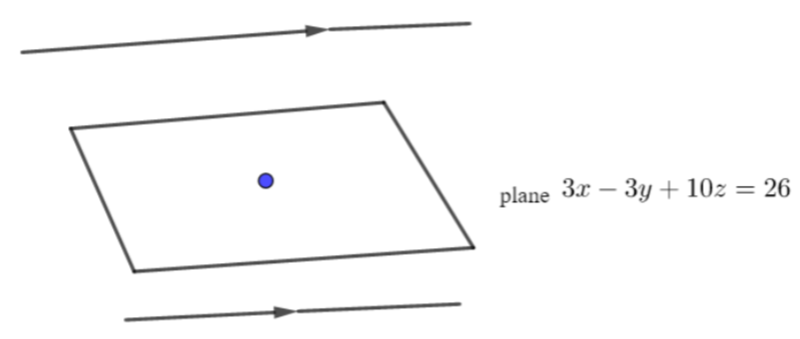
So, now how to find that this line is parallel to plane
$\begin{align}
& \Rightarrow 9\times 3+\left( -1 \right)\left( -3 \right)+\left( -3 \right)\left( 10 \right) \\
& \Rightarrow 27+3-30 \\
& \Rightarrow 0 \\
\end{align}$(By cosine direction)
This means it will be parallel
Now it become,

$\dfrac{x-1}{3}=\dfrac{y-2}{-3}=\dfrac{z+3}{10}=\lambda $
$\begin{align}
& x=3\lambda +1 \\
&\Rightarrow y=-3\lambda +2 \\
&\Rightarrow z=10\lambda -3 \\
\end{align}$
And equation of plane is $3x-3y+10z-26=0$
After simplifying the equation we will get,
$\begin{align}
  & 3\left( 3\lambda +1 \right)-3\left( -3\lambda +2 \right)+10\left( 10\lambda -3 \right)-26=0 \\
 & 9\lambda +3+9\lambda -6+100\lambda -30-26=0 \\
 &\Rightarrow 118\lambda =30+26+3 \\
 &\Rightarrow 118\lambda =59 \\
 &\Rightarrow 2\lambda =1 \\
 &\Rightarrow \lambda =\dfrac{1}{2} \\
\end{align}$
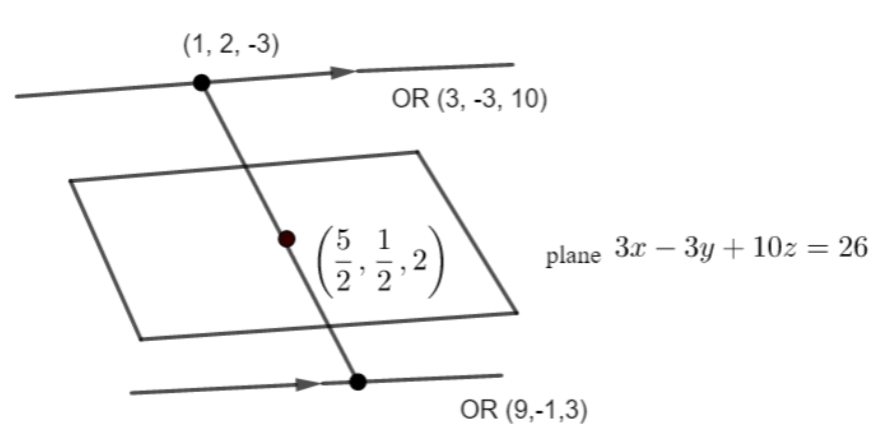
So, after putting in the equation we get the values $\left( \dfrac{5}{2},\dfrac{1}{2},2 \right)$
Now, we have midpoint and endpoint so finding the endpoint formula as let say (a=1, b=2, c=-3)
$\begin{align}
  & \dfrac{a+1}{2}=\dfrac{5}{2} \\
 &\Rightarrow a+1=5 \\
 &\Rightarrow a=4 \\
\end{align}$
X co-ordinate be 4
$\begin{align}
  &\Rightarrow \dfrac{b+2}{2}=\dfrac{1}{2} \\
 &\Rightarrow b+2=1 \\
 &\Rightarrow b=-1 \\
\end{align}$
Y co-ordinate be -1
$\begin{align}
  &\Rightarrow \dfrac{c-3}{2}=2 \\
 &\Rightarrow c-3=4 \\
 &\Rightarrow c=7 \\
\end{align}$
Z co-ordinate be 7
The lines are passing through (4, -1, 7) and directions are passing through (9, -1, -3)
$\dfrac{x-4}{9}=\dfrac{y+1}{-1}=\dfrac{z-7}{-3}$ this is the required line for the plane.
Hence the correct option is B.

Note: Alternate Method: (Shortcut method)
Given line is $\dfrac{x-1}{9}=\dfrac{y-2}{-1}=\dfrac{z+3}{-3}$………(1)
And the plane is $3x-3y+10z=26$…….(2)
Therefore, the direction ratios of the line are 9, -1, -3 and the direction ratios of the normal to the given plane are 3, -3, and 10.
Clearly, line (1) is parallel to the Plane (2)
Let Q be the image of the point P (1, 2, -3).
Consider,
 $\begin{align}
  &\Rightarrow Q=(\alpha ,\beta ,\gamma ) \\
 & now, \\
 &\Rightarrow \dfrac{\alpha -1}{3}=\dfrac{\beta -2}{-3}=\dfrac{\gamma +3}{10}=-2\left( \dfrac{3-6-30-26}{9+9+100} \right) \\
 &\Rightarrow \dfrac{\alpha -1}{3}=\dfrac{\beta -2}{-3}=\dfrac{\gamma +3}{10}=1 \\
 &\Rightarrow \alpha =4,\beta =-1,\gamma =7 \\
\end{align}$
Hence, the required image of the line w.r.t. the given plane is
$\dfrac{x-4}{9}=\dfrac{y+1}{-1}=\dfrac{z-7}{-3}$