Question

The equation of an altitude of an equilateral triangle is \[\sqrt{3}x+y=2\sqrt{3}\] and one of the vertices is \[\left( 3,\sqrt{3} \right)\] , then which of the given one is the orthocenter of the triangle?
\[\begin{align}
  & A.\left( 1,\sqrt{3} \right) \\
 & B.\left( 0,\sqrt{3} \right) \\
 & C.\left( 0,2 \right) \\
 & D.\text{none of these} \\
\end{align}\]

Answer 1

Hint: Firstly we have to check if the given point satisfies the equation. If it does not satisfy, it means that it lies upon the base of the equilateral triangle. Then we have to consider the equation of altitude and find the midpoint of the triangle. Now consider the slope equation and find out the equation of a side. And on summing up the equations, we get the orthocentre of the given triangle.

Complete step-by-step solution:
Now let us have a look about the orthocentre of an equilateral triangle. The orthocentre is the point at which the altitudes of a triangle intersect. And a triangle has three altitudes altogether.
Let us start finding the orthocentre of the given triangle.
Firstly, verify whether the given point \[\left( 3,\sqrt{3} \right)\] satisfies the given equation \[\sqrt{3}x+y=2\sqrt{3}\].
\[\begin{align}
  & \sqrt{3}x+y=2\sqrt{3} \\
 &\Rightarrow \sqrt{3}\left( 3 \right)+\sqrt{3}\ne 2\sqrt{3} \\
\end{align}\]
Hence we can conclude that it lies on the base of the triangle to which the altitude is drawn. Let \[B\] be the point and \[AD\] be the altitude.
\[\therefore \] \[BC\] is perpendicular to the altitude. The equation will be given as
\[\left( y-\sqrt{3} \right)=\dfrac{x-3}{\sqrt{3}}\]
\[\Rightarrow x=\sqrt{3}y\]
On substituting this in the equation of altitude, we get the midpoint of \[BC\] as \[\left( \dfrac{3}{2},\dfrac{\sqrt{3}}{2} \right)\].
\[\therefore \] \[B\] = \[\left( 3,\sqrt{3} \right)\] and the midpoint of \[BC\] is \[\left( \dfrac{3}{2},\dfrac{\sqrt{3}}{2} \right)\].
From this we can conclude that \[C= \left( 0,0 \right)\].
We know that the sides \[AB\] and \[AC\] make \[{{30}^{\circ }}\] with the altitude.
Considering the slope as \[m\] and the slope of altitude being \[-\sqrt{3}\], we get that
\[\tan \left( {{30}^{\circ }} \right) =\left| \dfrac{m+\sqrt{3}}{1-\sqrt{3}m} \right|.\]
\[\Rightarrow \pm \dfrac{1}{\sqrt{3}}=\dfrac{m+\sqrt{3}}{1-\sqrt{3}m}\]
\[\Rightarrow m=-\dfrac{1}{\sqrt{3}}\]or\[m=\infty \]
Considering \[m=-\dfrac{1}{\sqrt{3}}\] as the slope of, the equation would be
\[\left( y-\sqrt{3} \right)=\dfrac{-x+3}{\sqrt{3}}\]
On solving this, we get
\[x+\sqrt{3}=6\]
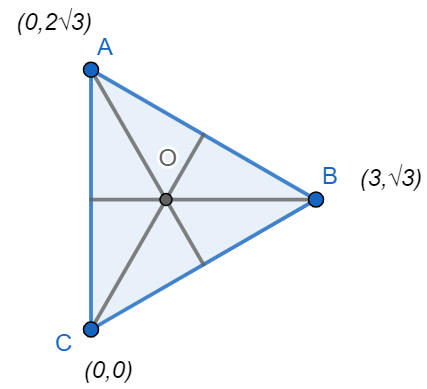
Solving the equations of altitude, we get \[A=\left( 0,2\sqrt{3} \right)\]
On summing up, we get
\[A=\left( 0,2\sqrt{3} \right)\],\[B=(3,\sqrt{3})\],\[C=\left( 0,0 \right)\]
We know that if we have three vertices of a triangle as $A\left({x_1},{y_1}\right)$, $B\left({x_2},{y_2}\right)$ and $C\left({x_3},{y_3}\right)$, Then the orthocentre of the triangle is
$\left(x,y\right)= \left(\dfrac{x_1+x_2+x_3}{3} \right),\left(\dfrac{y_1+y_2+y_3}{3}\right)$
Here we have $\left({x_1},{y_1}\right)=\left( 0,2\sqrt{3} \right)$, $\left({x_2},{y_2}\right)=B=(3,\sqrt{3})$ and $\left({x_3},{y_3}\right)=\left( 0,0 \right)$
Hence the orthocentre is-
\[O=\left( \dfrac{3}{3},\dfrac{3\sqrt{3}}{3} \right)\]
Hence the orthocentre of the triangle
\[\therefore O=\left( 1,\sqrt{3} \right)\]

Note: There is no direct formula to calculate the orthocentre of the triangle. It lies inside for an acute triangle and outside for an obtuse triangle. It is the intersection point of the altitudes of the triangle where altitude is nothing but the perpendicular line from one vertex to the opposite side of the triangle.