Question

The energy stored in capacitors is U when S is open. Now S is closed, the charge passed through S is Q, then
(A). $U=0,\,Q=2CE$
(B). $U=C{{E}^{2}},\,Q=0$
(C). $U=0,\,Q=\dfrac{7}{6}CE$
(D). $U=0,\,Q=\dfrac{2}{3}CE$

Answer 1

Hint: The following figure contains capacitors connected in series combination along with two batteries connected in parallel combination. We resolve the circuit by calculating both equivalent capacitance as well as equivalent voltage in the circuit and calculate the charge in the circuit. The energy depends on the capacitance and the square of the potential drop.

Formulas Used:
$\dfrac{1}{C}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}$
$Q'=C''V$

Complete step by step answer:

Since all the capacitors are in series combination, the charge will be equal. On resolving the circuit by replacing the combination with an equivalent capacitor we get,
$\begin{align}
  & \dfrac{1}{C}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}} \\
 & \Rightarrow \dfrac{1}{{{C}_{1}}}=\dfrac{1}{C}+\dfrac{1}{C} \\
 & \Rightarrow \dfrac{1}{{{C}_{1}}}=\dfrac{2}{C} \\
 & \therefore {{C}_{1}}=\dfrac{C}{2} \\
\end{align}$
Similarly,
$\begin{align}
  & \dfrac{1}{{{C}_{2}}}=\dfrac{1}{2C}+\dfrac{1}{2C} \\
 & \therefore {{C}_{2}}=C \\
\end{align}$

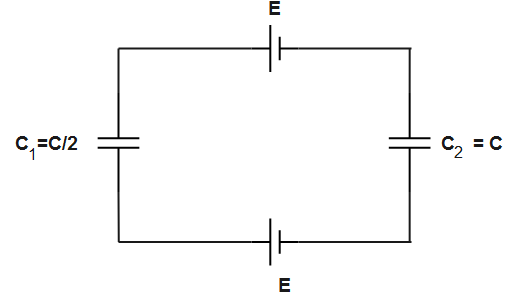
The equivalent capacitance in the above circuit is-
$\begin{align}
  & \dfrac{1}{C'}=\dfrac{1}{C}+\dfrac{2}{C} \\
 & \Rightarrow \dfrac{1}{C'}=\dfrac{3}{C} \\
 & \Rightarrow C'=\dfrac{C}{3} \\
\end{align}$
The equivalent capacitance of the whole circuit is $\dfrac{C}{3}$.
The batteries are connected in series, hence the equivalent emf in the circuit will be $E+E=2E$.
We know that,
$Q'=C''V$ - (1)
Here, $Q'$ is the charge flowing in a circuit
$C''$ is the capacitance
$V$ is the potential difference
In the above equation, we substitute given values to get the charge on capacitor with capacitance $C$,
$\begin{align}
  & Q'=\dfrac{C}{3}\times 2E \\
 & \Rightarrow Q'=\dfrac{2CE}{3} \\
\end{align}$
All capacitors are connected in series therefore, the charge flowing through them is same. Therefore, the charge flowing through each capacitor is $\dfrac{2CE}{3}$.
The charge that flows through the wire when switch S is closed is $\dfrac{2CE}{3}$.

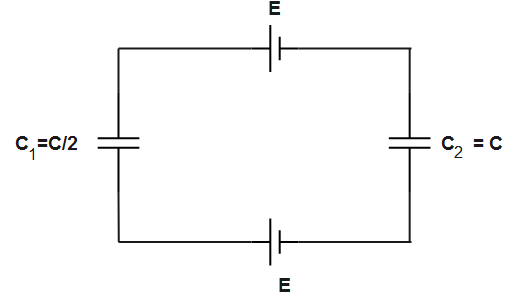
In the above figure, the plates of the capacitor are at the same potential that means there is no potential difference between the plates of the capacitor. Hence, there is no energy stored in the capacitors.
Therefore, the correct answer is option D.

Note: The combination of capacitors is analogous to the combination of resistors. Batteries can also be connected in series and parallel combination and their equivalent voltage depends on the emf as well as the internal resistance. The emf is the potential of the battery, it is always greater than the potential difference.