Question

The e/m ratio for electron was determined by:
A. JJ Thomson
B. Planck
C. Einstein
D. Schrodinger

Answer 1

Hint: According to classical electrodynamics, the value of the mass-to - charge ratio is that, when exposed to the same electric and magnetic fields, two particles with the same mass-to - charge ratio travel along the same direction in a vacuum. Its SI unit is kg / C.

Complete answer:
In the nineteenth century, J.J Thomson proposed Thomson’s Atomic Model discovered the electron to mark inception to the planet of subatomic particles. Once the electron was discovered, he continued his experiments to calculate the charge and therefore the mass of the electron. With the assistance of his experiments, he derived a formula for the calculation of charge to mass ratio of the electron.
The charge to mass ratio of the electron is given by:
${e}/{m=1.758820\times }\;{{10}^{11}}{C}/{kg}\;$
Where,
m = mass of an electron in kg = $9.10938356\times {{10}^{-31}}$ kg.
e = magnitude of the charge of an electron in coulombs = $1.602\times {{10}^{-19}}$ coulombs.
Experimental setup for the determination of charge to mass ratio of the electron.

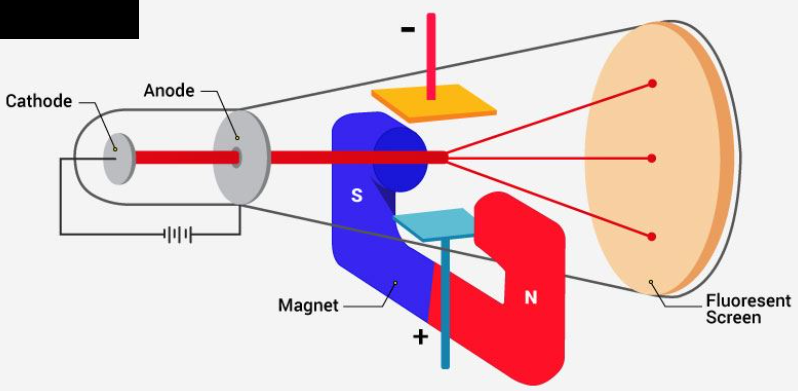
While completing the discharge tube experiment, Thomson observed that the particles of the cathode deviate from their path. He noticed the amount of deviation within the presence of an electrical or magnetic field depends on various related parameters. They are:
Particles with a greater magnitude of the charge experienced greater interaction with the electrical or magnetic field. Thus, they exhibited greater deflection.
Lighter particles experienced greater deflection. Thus, deflection is inversely proportional to the mass of the particle.
Deflection of the particle from their path is directly proportional to the strength of the electrical and therefore the magnetic flux present.
Let us now understand this with the assistance of his experimental observations.
The electrons deviated from their path and hit the cathode ray tube at point ‘x’ within the presence of a known field.
Similarly, an electron strikes the discharge tube at point ‘z’ when only the magnetic flux is present.
Thus, to form electrons continue on an equivalent path we'd like to balance the electrical and magnetic flux working on them.
Finally, based on the deflection of the electron, Thomson calculated the worth of charge to mass ratio of the electron.
Hence, the e/m ratio for electrons was determined by JJ Thomson.
So, the correct answer is “Option A”.

Note: Always remember, the charge to mass ratio of the electron is given by:
                   ${e}/{m=1.758820\times }\;{{10}^{11}}{C}/{kg}\;$
Mass of an electron (m) in kg = $9.10938356\times {{10}^{-31}}$ kg.
Magnitude of the charge of an electron (e) in coulombs = $1.602\times {{10}^{-19}}$ coulombs.
The electron is a low-mass, negatively charged particle. It can easily be deflected by passing close to others electrons or the positive nucleus of an atom.