Question

The element that shows greater ability to form $p\pi -p\pi $ multiple bonds is:
A. Si
B. Ge
C. Sn
D. C

Answer 1

Hint: The $p\pi -p\pi $ bond is formed when the collision occurs sideways and not head-on. So it completely depends on the size of the orbitals because the orbitals can overlap with each other from the sides only if they are small in size.

Complete step by step solution:
-There are 4 quantum numbers n, l, m and s. The principal quantum number (n) tells us about the shells of the atom. The azimuthal quantum number (l) tells us about the subshells of the atom. The magnetic quantum number (m) tells us about the orbitals of the atom and the spin quantum number (s) tells us about the orientation of the electrons in the orbital.
-Third quantum number is magnetic quantum number and is denoted by m. It gives us the exact orbitals. Its total value can be given as ${{n}^{2}}$ or as (2l+1) since it lies in the range (-l to +l). So, the p-subshell comes into picture when the value of n=2 and there are 3 orbitals for p-subshell since the value of l will be 1 for it. These orbitals are ${{p}_{x}},{{p}_{y}},{{p}_{z}}$. They form both sigma and pi bonds and their representations can be shown as

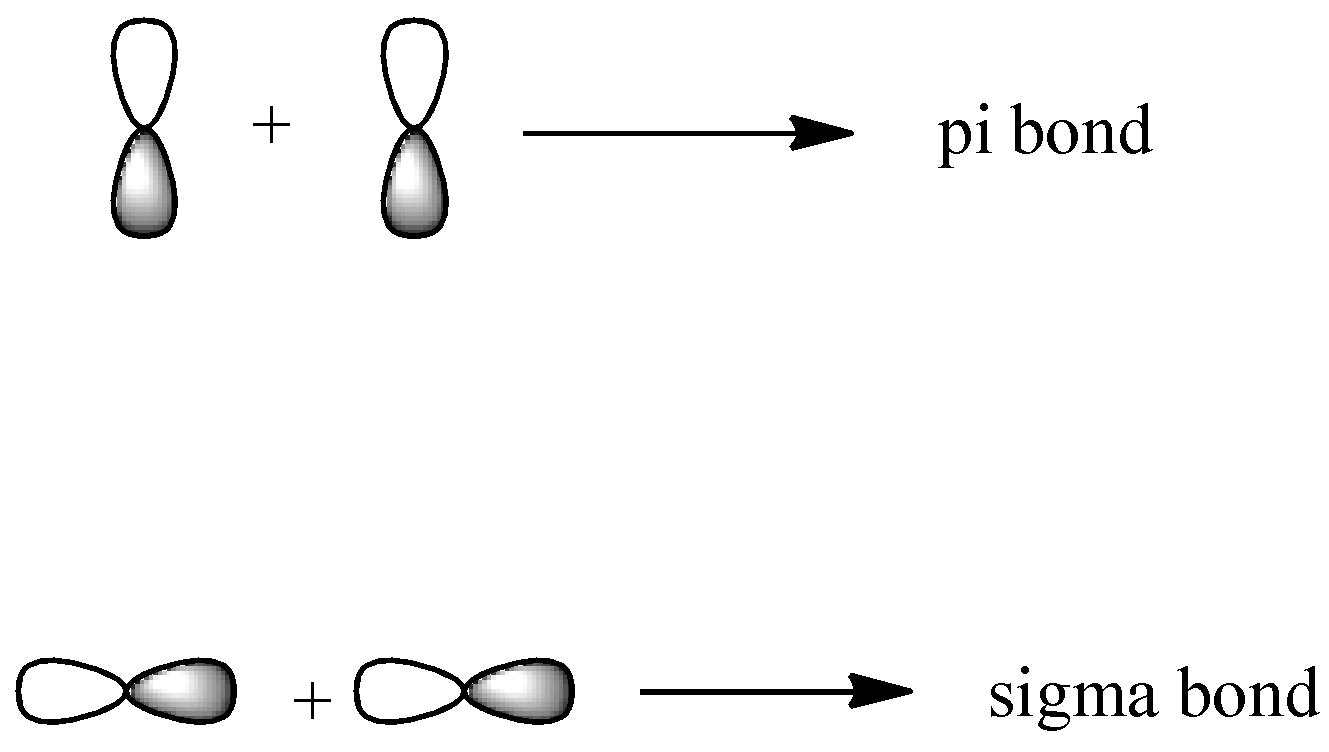
-If the orbital is very large, there will not be any effective overlapping between the orbitals to form the pi bond and the bond will not be able to be stabilized. So the orbitals with bigger size cannot form the $p\pi -p\pi $ multiple bonds.
-In the given options, we see that all the elements belong to the same group. We know the size increases down the group and so will the orbital size. Carbon is the smallest of all and so it will have the highest tendency to form $p\pi -p\pi $ multiple bonds.

Thus the correct option is D.

Note: The size effect does not count in sigma bonds as it is formed by head-on collision of the orbitals. So the orbitals have complete interaction with each other no matter what their size is. So they can be formed for all elements. Delta bonds also depend on the size factor like the pi bond.