Question

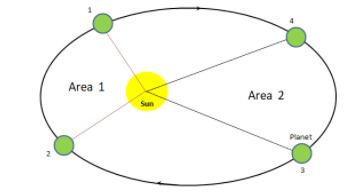
The drawing represents a planet orbiting some star. The planet is closer to the star as it moves from point 1 to point 2 than it is when it moves from point 3 to point 4 in its orbit. The dotted line shows its orbital path.
If the time it takes the planet to get from point 1 to point 2 is equal to the time it takes the planet to get from point 3 to point 4 then which of the following statements is true, according to Kepler’s law of planetary motion?
$(A)$ The average speed as the planet travels from 1 to 2 is the same as when it travels from 3 to 4
$(B)$ Area 1 in the diagram is equal to area 2
$(C)$ Area 1 in the diagram is smaller than area 2
$(D)$ The planet moves further from 3 to 4 from 1 to 2
$(E)$ The average speed as the planet moves from 3 to 4 is greater than when the planet moves from 1 to 2.

Answer 1

Hint: This question can be solved by stating the three laws of Kepler’s planetary motion and then applying the most probable law to the question. The applicable law for this question mentions that the areal velocity is constant. So by using the formula of speed in terms of distance and time, and applying Kepler’s law in a given time the answer can be obtained. Then finally compare the answer obtained to the various options provided.

Formula used: $V = \dfrac{S}{t}$ where V is speed, S gives distance and t is time

Complete step-by-step solution:

There are three of Kepler’s laws of planetary motion
The orbit of every planet is elliptical with the sun at its focus.
According to the second law, an imaginary line that connects the sun and the planet sweeps equal area at equal times.
The third law states that the planet’s orbital period when squared is proportional to the semi-major axis of its orbit when cubed.
For this problem, the second law is the most applicable law
Using the second law, let’s solve this question
Suppose the areal velocity of the planet traveling the area from point 1 to 2 is V and the area covered is given by A$_1$
Then from the equation $V = \dfrac{S}{t}$ where V is speed, S gives distance and t is time
We get, \[V = \dfrac{{A{\;_1}}}{{\Delta t}}\]
Now suppose the velocity of the planet covering the area from point 3 to 4 is V’ and the area covered is given by A$_2$
Then \[V' = \dfrac{{A{\;_2}}}{{\Delta t}}\]
In a given time \[\Delta t\] and from Kepler’s second law of planetary motion, that is the areal velocity is constant,
We get\[\dfrac{{A{\;_1}}}{{\Delta t}} = \dfrac{{A{\;_2}}}{{\Delta t}}\]
That is \[A{\;_1} = A{\;_2}\]
So from this, we get the area $1$ in the diagram that is equal to the area $2$
$(A)$ By solving we have determined that the area covered is equal. Hence this option is wrong
$(B)$ Area 1 in the diagram is equal to area 2, this is the right option.
$(C)$ Since both, the areas are the same. This option is wrong.
$(D)$ The distance covered in a period is the same. Therefore this option is not right
$(E)$ By solving this, we have estimated that the area covered is equal. Hence this option is wrong
The right option is $(B)$.

Note: When solving this question if Kepler's law is not used, the steps can become complicated and your probability of solving the problem will be below. So the first impertinent thing to do is to find the most applicable law suitable for this question. Then by using a basic equation like distance= speed*time, problems of these types can easily be solved.