Question

The distance from the pitcher's mound to home plate is 18.4m. The mound is 0.2m above the level of the eld. A pitcher throws a fastball with an initial speed of 37.5m/s. What should be the angle (in degrees) between the ball's initial velocity and the horizontal if the ball is to cross the plate a height of 0.7m above the ground? (Neglect air resistance)
A. 1.93
B. 2
C. 3
D. 6

Answer 1

Hint: You could make a rough sketch of the given conditions. Then recall equations of motions and choose the apt one among them to solve the problem. Recall all the normal facts about the projectile motion so as to make it easier to solve the given problem. You could consider some part of the motion to find the angle.
Formula used:
Equation of motion,
${{v}^{2}}-{{u}^{2}}=2as$

Complete answer:
In the question we have the distance between pitchers mound and home plate given as 18.4m and we are told that the mound is 0.2m above the eld’s level. The initial velocity of the ball is given as 37.5m/s and it is also known to cross a plate that is at a height of 0.7m above the ground. We are asked to find the angle of the projectile neglecting air resistance using this information.
So, we are dealing with projectile motion.

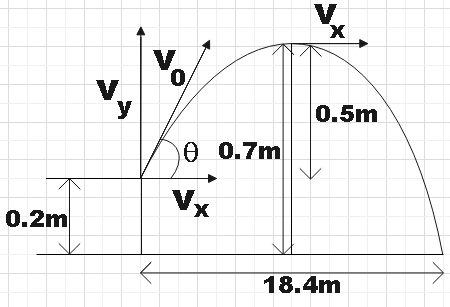
We have resolved the initial velocity into its horizontal and vertical components. Now, let us consider the vertical motion from the point of projection to the highest point. The vertical displacement then is,
$s=0.5m$
Now on applying Equation of motion,
${{v}^{2}}-{{u}^{2}}=2as$
$\Rightarrow 0-{{v}_{y}}^{2}=-2g\left( 0.7 \right)$
$\therefore {{v}_{y}}=\sqrt{2\times 9.8\times 0.7}=3.74$
Now, from the figure we see that,
$\sin \theta =\dfrac{{{v}_{y}}}{{{v}_{0}}}$
$\Rightarrow \sin \theta =\dfrac{3.74}{37.5}$
$\Rightarrow \theta ={{\sin }^{-1}}\left( \dfrac{3.74}{37.5} \right)$
$\therefore \theta ={{\sin }^{-1}}\left( 0.099 \right)=5.68{}^\circ \approx 6{}^\circ $
Therefore, we have found the angle of the projectile to be$6{}^\circ $ .

Hence, option D is found to be the correct answer.

Note:
For any projectile motion we know that the horizontal component of velocity remains constant throughout. Also, at the highest point the vertical component of velocity is zero but there we will still have the same horizontal velocity. For problems like this make sure that you draw a rough sketch of the given condition.