Question

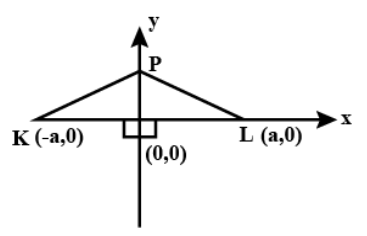
The diagram shows a straight line KL. P is a point which moves so that it is equidistant from the point K and point L. which of the following is the locus of P?
A)

B)

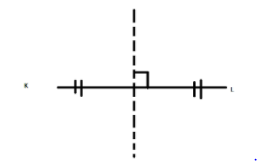
C)

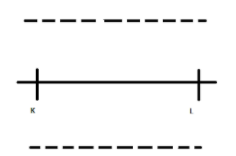
D)

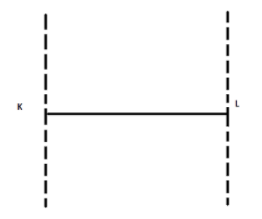
E)

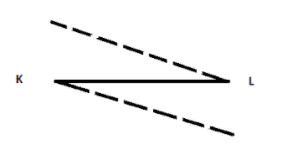
Answer 1

Hint: The point moves in such a way that the distance from point K and the point L is always the same. If we analyze our options and figures, we can see the line where the distance from the point from two sides is always equal. We will start by taking the origin at the midpoint of the line.

Complete step by step solution: Now, Let the midpoint of 'KL' be the origin. And let KL has a length of 2a units.

And also, Let, P be any pt. with coordinates\[(x,y)\].

The coordinates of K and L will respectively be, \[( - a,0)\]and\[(a,0)\].

So, now, KP\[ = {(x - ( - a))^2} + {(y - 0)^2}\]\[ = {(x + a)^2} + {y^2}\]

And PL\[ = {(a - x)^2} + {(0 - y)^2}\]\[ = {(a - x)^2} + {y^2}\]

According to the problem, KP=PL,

So we get, \[{(x + a)^2} + {y^2} = {(a - x)^2} + {y^2}\]
\[ \Rightarrow {(x + a)^2} = {(a - x)^2}\]
The only solution this is possible is, \[x = 0\], which is the equation of the y-axis.

So, locus of 'P' is the perpendicular bisector of KL. Which is an option (a).

Note: We can also consider the line KL along the line of the y-axis. Then we will find the required line over the x-axis. Locus is one of the tough topics in coordinate geometry. Problems like this will help us to understand the locus properly. It simply says a point will move with a given condition find its path. To solve such problems we need to counter all the points which will satisfy the given condition.