Question

The co-ordinates of three-point O, A, B are $(0,0)$ , $(0,4)$ and $(6,0)$ respectively. A point P moves so that area of triangle POA is always twice the area of triangle POB. Find the equation of both parts of locus of P.
 A. $(x - 3y)(x - 3y) = 0$
 B. $(x + 3y)(x + 3y) = 0$
 C. $(x - 3y)(x + 3y) = 0$
 D. None of these

Answer 1

Hint: First we’ll assume any point P, using this point we’ll calculate the area of triangle POA and triangle POB, now we have given a condition in the areas of both triangles as the area of triangle POA is always twice the area of triangle POB. Simplifying this we’ll get the required equations.

Complete step by step answer:

Given data: O$(0,0)$ , A$(0,4)$ and B$(6,0)$
Area of triangle POA=2(Area of triangle POB)
Let P be any point $\left( {x,y} \right)$

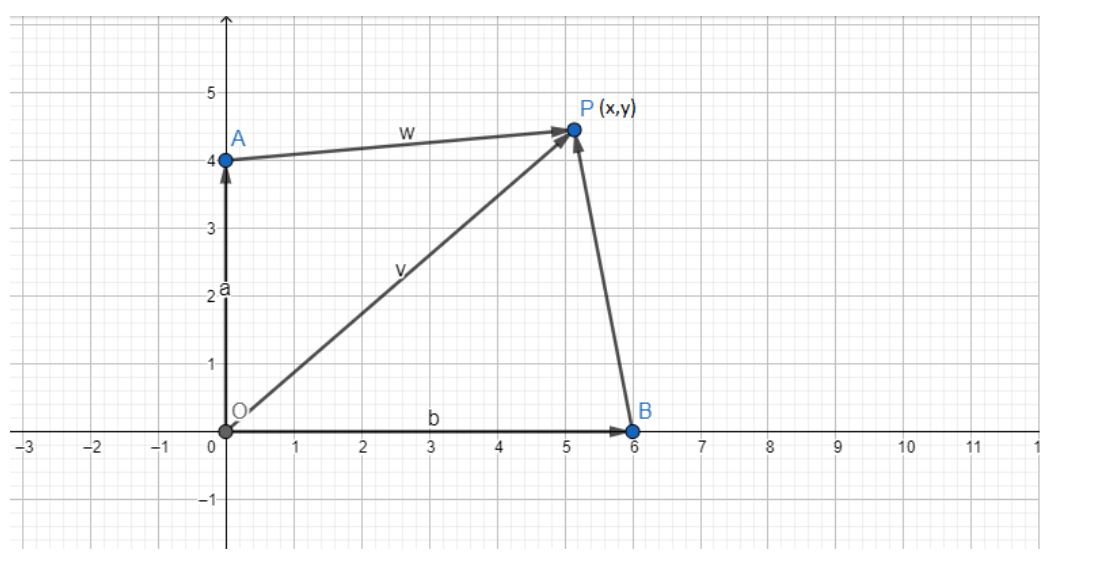
From the graph, we can see that OA and OB are on the coordinate axis hence
The height of any point from OA will be the abscissa part(x-part) of the point,
Similarly, the height of any point from OB will be the ordinate part(y-part) of the point,
We know that area of any triangle $ = \dfrac{1}{2}(base)(height)$
It is given that, area of triangle POA=2(Area of triangle POB)
 $ \Rightarrow \left| {\dfrac{1}{2}(OA)(x)} \right| = \left| {2 \times \dfrac{1}{2}(OB)(y)} \right|$
As OA is 4 and OB is 6, we get,
 $ \Rightarrow \left| {\dfrac{1}{2}4(x)} \right| = \left| {6(y)} \right|$
On Multiplying both sides by $\dfrac{1}{2}$, we get,
 $ \Rightarrow \left| x \right| = \left| {3y} \right|$
On removing Modulus we get,
 $ \Rightarrow x = \pm 3y$
 $ \Rightarrow x \mp 3y = 0$
Therefore both parts are $(x - 3y)(x + 3y) = 0$
Therefore,option(C) is correct.

Note: Here we can also use the formula for the area of the triangle when all the vertices of a triangle are given let say $\left( {{x_1},{y_1}} \right)$ , $\left( {{x_2},{y_2}} \right)$ and $\left( {{x_3},{y_3}} \right)$ then the area of the triangle will be
Area of triangle $ = \dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]$
But this method will take a longer period to get the answer so for this particular method try doing by the above method as it is much easier, and understanding and takes a shorter time to solve as we have used the formula for the area of the triangle i.e.
Area of any triangle $ = \dfrac{1}{2}(base)(height)$