Question

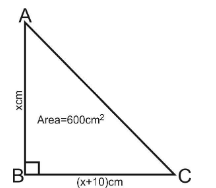
The area of a right angled triangle is $ 600c{m^2} $ . If the base of the triangle exceeds the altitude by $ 10 $ cm, find the dimensions of the triangle.

Answer 1

Hint: In this problem as base exceeds altitude, hence first let base be ‘x’ and then using it writing altitude in terms of ‘x’. Using both base and altitude in area formula to calculate value of unknown variable ‘x’ and so required values asked in a given problem.
Formulas used: Area of the triangle having base and altitude given as $ \dfrac{1}{2} \times base \times altitude $ , Pythagoras theorem formula $ {\left( {Hyp.} \right)^2} = {\left( {Perp.} \right)^2} + {\left( {Base} \right)^2} $

Complete step-by-step answer:
Let the altitude of the right angle triangle be ‘x’
Then, base of right angle triangle which exceeds altitude by $ 10 $ cm is given as: $ x + 10 $
Area of right angle triangle is given = $ 600c{m^2} $

We know that area of right angle triangle = $ \dfrac{1}{2} \times base \times altitude $
Substituting values in above formula we have,’
 $ 600 = \dfrac{1}{2} \times \left( x \right) \times \left( {x + 10} \right) $
Simplifying right hand side of the above equation we have
 $
  600 = \left( {\dfrac{{{x^2} + 10x}}{2}} \right) \\
   \Rightarrow 2 \times 600 = {x^2} + 10x \\
   \Rightarrow 1200 = {x^2} + 10x \;
  $
Or we can write as
 $ {x^2} + 10x - 1200 = 0 $
Solving, above formed quadratic equation by middle term splitting method.
 $
  {x^2} + 40x - 30x - 1200 = 0 \\
   \Rightarrow x\left( {x + 40} \right) - 30\left( {x - 40} \right) = 0 \\
   \Rightarrow \left( {x + 40} \right)\left( {x - 30} \right) = 0 \\
   \Rightarrow x + 40 = 0\,\,\,or\,\,\,x - 30 = 0 \\
  \Rightarrow x = - 40\,\,\,or\,\,\,x = 30 \;
  $
Where $ x = - \,40 $ is not possible.
Therefore the base of the right angle triangle is $ 30\,cm $ .
Altitude of right angle triangle is $ \left( {x + 10} \right) = \left( {30 + 10} \right) $
Therefore, the altitude of the triangle is $ 40cm $ .
To find the third side of the triangle we apply Pythagora's theorem which states that in right angle triangle square of hypotenuse is equal to sum of square of other two sides.
i.e. $ {\left( {Hyp} \right)^2} = {\left( {Perp} \right)^2} + {\left( {Base} \right)^2} $
Substituting values in above formula we have
 $
  {\left( {Hyp.} \right)^2} = {\left( {30} \right)^2} + {\left( {40} \right)^2} \\
   \Rightarrow {\left( {Hyp.} \right)^2} = 900 + 1600 \\
   \Rightarrow {\left( {Hyp} \right)^2} = 2500 \\
   \Rightarrow {\left( {Hyp} \right)^2} = {\left( {50} \right)^2} \;
 $
 $ \Rightarrow Hyp = 50 $
Therefore, hypotenuse of right angle triangle is $ 50cm. $
Hence, from above we see that the dimensions of the given right angle are $ 30cm,\,\,\,40cm\,\,and\,\,50cm $ respectively.

Note: For questions in which there is a hint of depending conditions students must be very careful while considering which part will be considered as unknown variable(x) and which part will be written in terms of considered unknown variable(x) to simplify to get required solution of the problem.