Question

The area of a circle inscribed in an equilateral triangle is \[154\text{ c}{{\text{m}}^{\text{2}}}\]. The side of the triangle is:
(a) \[7\sqrt{3}\]
(b) \[14\sqrt{3}\]
(c) \[5\sqrt{3}\]
(d) \[10\sqrt{2}\]

Answer 1

Hint: In this question, first of all, draw the diagram to get a clear idea about the question. Then divide the equilateral triangle into three parts and write the area of each part in terms of sides of the triangle and radius of the circle. Also, write the total area of the equilateral triangle, i.e. \[\dfrac{\sqrt{3}}{4}{{a}^{2}}\]. Equate both of these to get the value of sides of the triangle.

Complete step-by-step answer:
Here, we are given that the area of the circle inscribed in an equilateral triangle is \[154\text{ c}{{\text{m}}^{\text{2}}}\]. We have to find the side of the triangle.
First of all, we know that the equilateral triangle is a triangle in which the length of all the sides is equal and each interior angle is of \[{{60}^{o}}\].

Let us consider the condition given in question diagrammatically.

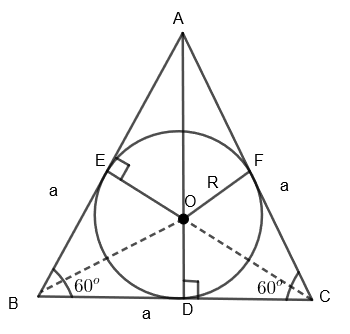
In the above diagram, ABC is an equilateral triangle with each side equal to ‘a’ and a circle is inscribed in it whose radius is ‘R’.
Here, we are given that area of the circle \[=154\text{ c}{{\text{m}}^{2}}\].
We know that the area of the circle \[=\pi {{R}^{2}}\]
So, we get, \[\pi {{R}^{2}}=154\text{ c}{{\text{m}}^{2}}\]
By substituting \[\pi =\dfrac{22}{7}\], we get,
\[\dfrac{22}{7}{{R}^{2}}=154\]
Or, \[{{R}^{2}}=\dfrac{7}{22}\times 154\]
By simplifying the above equation, we get,
\[{{R}^{2}}=49\]
By taking square root on both the sides, we get,
R = 7 cm.

Now, we know that the area of the equilateral triangle, \[\Delta \text{ABC = }\dfrac{\sqrt{3}}{4}{{a}^{2}}....\left( i \right)\]

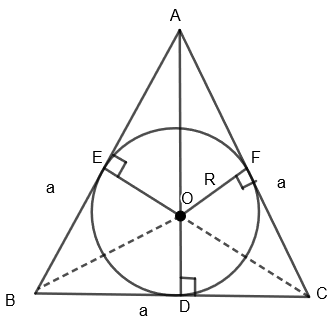
Here AB = AC = BC = a and OE = OF = OD = R
Also, we can say that area of the equilateral triangle
\[\Delta \text{ABC = area of }\left( \Delta AOB+\Delta AOC+\Delta BOC \right)....\left( ii \right)\]
We know that the area of the triangle \[=\dfrac{1}{2}\]\[\times \left( \text{Base of the triangle} \right)\times \left( \text{Height of the triangle} \right)\]
Here, we can see that OE, OF, and OD are the height of the triangles \[\Delta AOB,\text{ }\Delta AOC\text{ }and\text{ }\Delta BOC\]. So, we get,
\[\text{Area of }\Delta \text{AOB=}\dfrac{1}{2}AB\times OE=\dfrac{1}{2}\times a\times R\]
\[\text{Area of }\Delta \text{AOC=}\dfrac{1}{2}AC\times OF=\dfrac{1}{2}\times a\times R\]
\[\text{Area of }\Delta B\text{OC=}\dfrac{1}{2}BC\times OD=\dfrac{1}{2}\times a\times R\]
By substituting these values in equation (ii), we get,
\[\text{Area of equilateral }\Delta \text{ABC=}\dfrac{1}{2}aR+\dfrac{1}{2}aR+\dfrac{1}{2}aR=\dfrac{3}{2}aR....\left( iii \right)\]
Now by equating equation (i) and (iii), we get,
\[\dfrac{\sqrt{3}}{4}{{a}^{2}}=\dfrac{3}{2}aR\]
By dividing \[\dfrac{3}{2}a\] on both the sides, we get,
\[R=\dfrac{\sqrt{3}{{a}^{2}}.2}{4.3a}=\dfrac{a}{2\sqrt{3}}\]
We know that R = 7 cm.
By substituting the value of R, we get,
\[7=\dfrac{a}{2\sqrt{3}}\]
By cross multiplying the above equation, we get
\[a=14\sqrt{3}\text{ cm}\]
So, we have got the side of the triangle as \[14\sqrt{3}\text{ cm}\].
Hence option (b) is the right answer.

Note:
In this question, we can see that a circle is inscribed in the triangle, which means this circle is incircle of the triangle. So students can directly remember that inradius of the equilateral triangle is \[\dfrac{1}{2\sqrt{3}}\] times the side of the triangle that is \[R=\dfrac{a}{2\sqrt{3}}\]. Here, R is the inradius of the given incircle.